Giải Toán lớp 6 trang 43 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với giải Toán lớp 6 trang 43 Tập 1 trong Bài 13: Bội chung. Bội chung nhỏ nhất Toán lớp 6 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán lớp 6 trang 43.

Giải Toán lớp 6 trang 43 Tập 1 Chân trời sáng tạo

Thực hành 6 trang 43 Toán lớp 6 Tập 1:

1) Quy đồng mẫu các phân số sau:

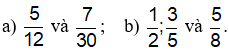
2) Thực hiện các phép tính sau: 

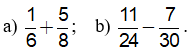
Lời giải:

1) 

a) 12 = 2².3, 30 = 2.3.5;

Các thừa số chung và riêng là 2, 3, 5.

Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất: 2².3.5 = 60.

Khi đó: BCNN(12, 30) = 60

60 : 12 = 5; 60 : 30 = 2. Do đó:

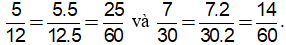
b) 2 = 2, 5 = 5, 8 = 2³

Các thừa số chung và riêng là 2, 5.

Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất: 2³.5 = 40.

Khi đó: BCNN(2, 5, 8) = 40

40:2 = 20; 40:5 = 8; 40:8 = 5. Do đó:

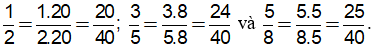
2) 

a) Ta có BCNN(6,8) = 24.

24: 6 = 4; 24:8 = 3. Do đó

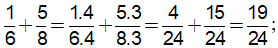
b) Ta có BCNN(24, 30) = 120.

120:24 = 5; 120:30 = 4. Do đó:

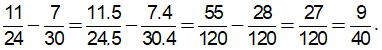
Bài 1 trang 43 Toán lớp 6 Tập 1:

Tìm:

a) BC(6, 14);                b) BC(6, 20, 30);

c) BCNN(1, 6);           d) BCNN(10, 1, 12);

e) BCNN(5, 14).

Lời giải:

a) Ta có: 6 = 2.3; 14 = 2.7 ⇒ BCNN(6,14) = 2.3.7 = 42.

Khi đó tập hợp bội chung của 6 và 14 là tập hợp bội của 42:

BC(6, 14) = B(42) = {0; 42; 84; 126; …}.

b) Ta có: 6 = 2.3; 20 =2².5; 30 = 2.3.5 ⇒ BCNN(6, 20, 30) = 2².3.5 =60

Khi đó tập hợp bội chung của 6, 20 và 30 là tập hợp bội của 60:

BC(6, 20, 30) = B(60) = {0; 60; 120; 180; …}.

c) Vì 1 và 6 là hai số nguyên tố cùng nhau nên BCNN(1, 6) = 1.6 = 6.

d) Ta có: BCNN(10, 1, 12) = BCNN(10, 12)

Phân tích 10 và 12 ra thừa số nguyên tố: 10 = 2.5, 12 = 2².3.

Suy ra BCNN(10, 12) = 2².3.5 = 60.

Vậy BCNN(10, 12) = 2².3.5 = 60.

e) Vì 5 và 14 là hai số nguyên tố cùng nhau nên BCNN(5, 14) = 5.14 = 70. 

Bài 2 trang 43 Toán lớp 6 Tập 1:

a) Ta có BCNN(12, 16) = 48. Hãy viết tập hợp A các bội của 48. Nhận xét về tập hợp BC(12, 16) và tập hợp A.

b) Để tìm tập hợp bội chung của hai số tự nhiên a và b, ta có thể tìm tập hợp các bội của BCNN(a, b). Hãy vận dụng để tìm tập hợp các bội chung của:

i.24 và 30;              ii. 42 và 60;                       

iii. 60 và 150;        iv.28 và 35.

Lời giải:

a) Các bội của 48 là 0, 48, 96, 144, 196,…

Do đó: A = {0; 48; 96; 144; 192;…}

BC(12, 16) = {0; 48; 96; 144; 192;…}

* Nhận xét: Tập hợp BC(12, 16) chính là tập hợp A.

b) 

i) Ta có: 24 = 2³.3; 30 = 2.3.5.

Suy ra BCNN(24,30) = 2³.3.5 = 12=.

Vậy BC(24, 30) = B(120) = {0; 120; 240; 360; 480; …}

ii) Ta có: 42 = 2.3.7; 60 =2².3.5.

Suy ra BCNN(42,60) = 2².3.5.7 = 420.

Vậy BC(42, 60) = B(42) = {0; 420; 840; 1260; …}.

iii) Ta có: 60 = 2².3.5; 150 = 2.3.5²

⇒ BCNN( 60, 150) = 2².3.5² = 300.

 BC(60, 150) = B(300) = {0; 300; 600; 900; …}.

iv) Ta có:  

⇒ BCNN( 28,35) = 2².5.7 =140.

BC(28,35) = B(140) = {0; 140; 280; 420;...}

Bài 3 trang 43 Toán lớp 6 Tập 1:

Quy đồng mẫu số các phân số sau (có sử dụng bội chung nhỏ nhất):

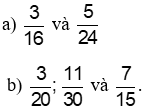
Lời giải:

a) 16 = 2⁴, 24 = 2³.3

Khi đó BCNN(16, 24) = 2⁴.3 = 48.

48:16 = 3; 48:24 = 2. Do đó:

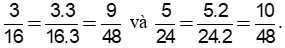
b) 20 = 2².5; 30 = 2.3.5; 60 = 2².3.5.

Khi đó BCNN(20, 30, 15) = 2².3.5 = 60.

60:20 = 3; 60:30 = 2; 60:15 = 4. Do đó:

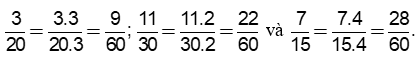
Lời giải bài tập Toán lớp 6 Bài 13: Bội chung. Bội chung nhỏ nhất Chân trời sáng tạo hay khác:

• Giải Toán 6 trang 40 Tập 1

• Giải Toán 6 trang 42 Tập 1

• Giải Toán 6 trang 44 Tập 1