Giải Toán lớp 6 trang 7 Tập 1 Kết nối tri thức
Haylamdo biên soạn và sưu tầm với giải Toán lớp 6 trang 7 Tập 1 trong Bài 1: Tập hợp Toán lớp 6 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 6 trang 7.
Giải Toán 6 trang 7 Tập 1 Kết nối tri thức
Câu hỏi trang 7 Toán lớp 6 Tập 1: Khi mô tả tập hợp L các chữ cái trong từ NHA TRANG bằng cách liệt kê các phần tử, bạn Nam viết:
L = {N; H; A; T; R; A; N; G}
Theo em, bạn Nam viết đúng hay sai?
Lời giải:
Bạn Nam viết sai vì theo cách mô tả của tập hợp thì mỗi phần tử chỉ được viết một lần nhưng ở đây chữ cái A, N xuất hiện hai lần.
Cách viết đúng là: L = {N; H; A; T; R; G}.
Luyện tập 2 trang 7 Toán lớp 6 Tập 1: Viết các tập hợp sau bằng cách liệt kê các phần tử của chúng:
A = {x ∈ ℕ | x < 5};
B = {x ∈ ℕ* | x < 5}.
Lời giải:
Chú ý: kí hiệu ℕ là tập hợp các số tự nhiên và ℕ* là tập hợp các số tự nhiên khác 0.
+) Ta có: A = { x ∈ ℕ | x < 5 }
Trong tập hợp A, ta thấy x ∈ ℕ và x < 5 nên x là các số tự nhiên nhỏ hơn 5, đó là: 0; 1; 2; 3; 4.
Do đó ta viết: A = {0; 1; 2; 3; 4}.
+) Ta có: B = {x ∈ ℕ* | x < 5}
Trong tập hợp B, ta thấy x ∈ ℕ* và x < 5 nên x là các số tự nhiên khác 0 và nhỏ hơn 5, đó là: 1; 2; 3; 4
Do đó ta viết: B = {1; 2; 3; 4}.
Luyện tập 3 trang 7 Toán lớp 6 Tập 1: Gọi M là tập hợp các số tự nhiên lớn hơn 6 và nhỏ hơn 10.
a) Thay dấu “?” bằng dấu ∈ hoặc ∉: 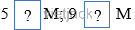
b) Mô tả tập hợp M bằng hai cách.
Lời giải:
a) Nhận thấy các số tự nhiên lớn hơn 6 và nhỏ hơn 10 là các số: 7; 8; 9
Nên tập hợp M gồm các số: 7, 8, 9
Do đó: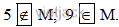
b) Do đó ta có mô tả tập hợp M theo hai cách như sau:
Cách 1: Liệt kê các phần tử của tập hợp
M = {7; 8; 9}.
Cách 2: Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp
M = {x ∈ ℕ | 6 < x < 10}
Bài 1.1 trang 7 Toán lớp 6 Tập 1: Cho hai tập hợp:
A = {a; b; c; x; y} và B = {b; d; y; t; u; v}.
Dùng kí hiệu “∈” hoặc “∉” để trả lời các câu hỏi: Mỗi phần tử a, b, x, u thuộc tập nào và không thuộc tập hợp nào?
Lời giải:
+) Tập hợp A có chứa phần tử a, hay a thuộc tập A và ta viết a ∈ A
Tập hợp B không chứa phần tử a, hay a không thuộc tập B và ta viết a ∉ B
+) Tập hợp A có chứa phần tử b, hay b thuộc tập A và ta viết b ∈ A
Tập hợp B có chứa phần tử b, hay b thuộc tập B và ta viết b ∈ B
+) Tập hợp A có chứa phần tử x, hay x thuộc tập A và ta viết x ∈ A
Tập hợp B không chứa phần tử x, hay x không thuộc tập B và ta viết x ∉ B
+) Tập hợp A không chứa phần tử u, hay u không thuộc tập A và ta viết u ∉ A
Tập hợp B có chứa phần tử u, hay u thuộc tập B và ta viết u ∈ B.
Bài 1.2 trang 7 Toán lớp 6 Tập 1: Cho tập hợp
U = {x ∈ ℕ | x chia hết cho 3}.
Trong các số 3; 5; 6; 0; 7 số nào thuộc và số nào không thuộc tập hợp U?
Lời giải:
Ta có: U = {x ∈ ℕ | x chia hết cho 3}
Khi đó ta thấy U là tập hợp các số tự nhiên x, sao cho x chia hết cho 3.
Vì x chia hết cho 3 nên các số chia hết cho 3 trong các số đã cho là: 3; 6; 0
Do đó: 3 ∈ U; 5 ∉ U; 6 ∈ U; 0 ∈ U; 7 ∉ U.
Bài 1.3 trang 7 Toán lớp 6 Tập 1: Bằng cách liệt kê các phần tử, hãy viết các tập hợp sau:
a) Tập hợp K các số tự nhiên nhỏ hơn 7;
b) Tập hợp D tên các tháng (dương lịch) có 30 ngày;
c) Tập hợp M các chữ cái tiếng Việt trong từ “ĐIỆN BIÊN PHỦ”.
Lời giải:
a) Các số tự nhiên nhỏ hơn 7 là: 0; 1; 2; 3; 4; 5; 6
Do đó tập hợp K gồm các phần tử: 0; 1; 2; 3; 4; 5; 6
Vì vậy, ta viết: K = {0; 1; 2; 3; 4; 5; 6}.
b) Ta đã biết các tháng dương lịch có 30 ngày là: Tháng 4; Tháng 6; Tháng 9; Tháng 11
Do đó tập hợp D gồm các phần tử: Tháng 4; Tháng 6; Tháng 9; Tháng 11
Vì vậy, ta viết: D = {Tháng 4; Tháng 6; Tháng 9; Tháng 11}.
c) Các chữ cái tiếng Việt trong từ “ĐIỆN BIÊN PHỦ” gồm Đ, I, Ê, N, B, I, Ê, N, P, H, U
Trong các chữ cái trên, chữ I được xuất hiện 2 lần, chữ Ê cũng được xuất hiện 2 lần, chữ N xuất hiện 2 lần nhưng ta chỉ viết trong tập hợp mỗi chữ một lần, ta có tập hợp các chữ cái M = {Đ; I; Ê; N; B; P; H; U}.
Lời giải bài tập Toán lớp 6 Bài 1: Tập hợp Kết nối tri thức hay khác:

