Giải Toán lớp 6 Luyện tập chung trang 57 - Kết nối tri thức
Haylamdo biên soạn và sưu tầm lời giải bài tập Toán lớp 6 Luyện tập chung trang 57 sách Kết nối tri thức với cuộc sống đầy đủ, chính xác nhất giúp các bạn làm bài tập Toán 6 nhanh nhất.
Giải Toán 6 Luyện tập chung trang 57 - Kết nối tri thức
Giải bài tập
Bài 8.19 trang 57 Toán lớp 6 Tập 2: Cho bốn điểm phân biệt A, B, C và D, trong đó không có ba điểm nào thẳng hàng.
a) Có bao nhiêu đường thẳng đi qua hai trong bốn điểm đã cho? Kể tên các đường thẳng đó.
b) Có bao nhiêu tia với gốc là một trong bốn điểm đã cho? Đó là những đoạn thẳng nào?
c) Có bao nhiêu đoạn thẳng có hai mút là hai trong bốn điêm đã cho? Đó là những đoạn thẳng nào?
Lời giải:
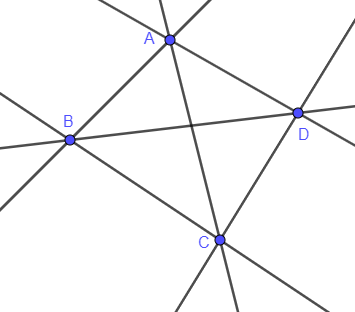
a) Có 6 đường thẳng đi qua hai trong bốn điểm đã cho
Tên các đường thẳng đó là: AB, AC, AD, BC, BD, CD.
b. Có 12 tia với gốc là một trong bốn điểm đã cho và đi qua một trong ba điểm còn lại
Đó là những tia: AB, AD, AC, BA, BC, BD, DA, DB, DC, CA, CB, CD.
c. Có 6 đoạn thẳng có hai mút là hai trong bốn điểm đã cho
Đó là những đoạn thẳng: AB, AD, AC, BC, BD, DC.
Bài 8.20 trang 57 Toán lớp 6 Tập 2: Cho ba điểm A, B, C cùng nằm trên đường thẳng d sao cho B nằm giữa A và C.
Hai điểm D và E không thuộc d và không cùng thẳng hàng với điểm nào trong các điểm A, B và C.
a) Có bao nhiêu đường thẳng, mỗi đường thẳng đi qua ít nhất hai trong năm điểm đã cho?
b) Tìm trên đường thẳng d điểm G sao cho ba điểm D, E, G thẳng hàng. Có phải khi nào cũng tìm được điểm G như thế hay không?
Lời giải:
a)
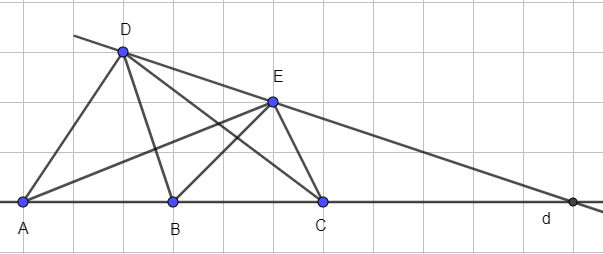
Có 8 đường thẳng là: AB (hay BC, AC); AD; AE; BD; BE; CD; CE; DE.
b)
Vẽ đường thẳng DE.
+) Nếu đường thẳng DE cắt đường thẳng d tại G thì ba điểm D, E, G thẳng hàng như hình vẽ dưới:
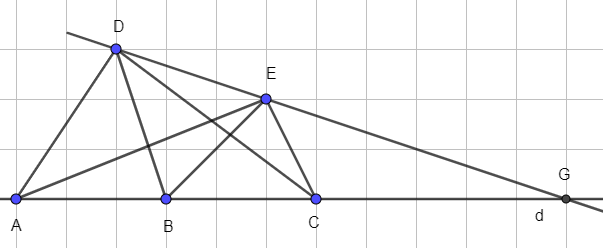
+) Nếu đường thẳng DE song song với với d thì không tìm được được G nào thỏa mãn G nằm trên đường thẳng d mà D, E, G thẳng hàng, minh họa bởi hình vẽ:
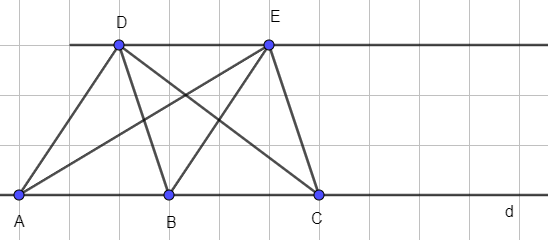
Bài 8.21 trang 57 Toán lớp 6 Tập 2: Cho điểm M trên tia Om sao cho OM = 5 cm. Gọi N là điểm trên tia đối của tia Om và cách O một khoảng bằng 7cm.
a) Vẽ hình và tính độ dài đoạn thẳng MN.
b) Gọi K là trung điểm của đoạn thẳng MN. Tính độ dài các đoạn thẳng MK và OK.
c) Điểm K thuộc tia nào trong hai tia OM và ON?
Lời giải:

a) Vì M, N là hai điểm thuộc hai tia đối nhau nên ta có điểm O nằm giữa hai điểm M và N nên ta có:
MN = ON + OM
Thay số: OM = 5cm; ON = 7cm nên MN = 5 + 7 = 12 (cm)
Vậy MN = 12cm.
b. Vì K là trung điểm của đoạn MN nên ta có:
KM = KN = MN: 2 = 12: 2 = 6 (cm)
Trên cùng mặt phẳng có bờ là tia đối của tia Om, ta có MO < MK (5 < 6) nên điểm O nằm giữa hai điểm M và K nên OK + OM = KM
Thay số: KM = 6 cm; OM = 5 cm, ta có:
OK + 5 = 6
OK = 6 – 5 = 1 (cm)
Vậy MK = 6cm; OK = 1cm.
c. Trên nửa mặt phẳng có bờ là tia đối của tia Om có: OK < ON (do 1 < 7) nên K thuộc tia ON.
Bài 8.22 trang 57 Toán lớp 6 Tập 2: Cho hai điểm phân biệt A và B cùng nằm trên tia Ox sao cho OA = 4 cm, OB = 6 cm. Gọi M là trung điểm của đoạn thẳng AB. Tính độ dài đoạn thẳng OM.
Lời giải:

Vì trên nửa mặt phẳng có bờ là tia Ox có OA < OB (4 < 6) nên điểm A nằm giữa hai điểm O và B nên ta có: OA + AB = OB
Thay số: OB = 6 cm ; A = 4 cm, ta được:
4 + AB = 6
AB = 6 – 4
AB = 2 cm
Vì M là trung điểm của AB nên ta có: MA = MB = AB: 2=1 cm
Vì trên nửa mặt phẳng có bờ là tia Ox có: MB < BO (1 < 6) nên điểm M nằm giữa hai điểm O và B, ta có: OM + MB = OB
Thay số: MB =1 cm; OB = 6 cm ta được:
OM + 1 = 6
OM = 6 – 1
OM = 5cm
Vậy độ dài đoạn thẳng OM dài 5cm.
Hoặc ta có thể làm theo cách sau:
Trên nửa mặt phẳng có bờ là tia Ox có: Vì M là trung điểm của đoạn thẳng AB, A nằm giữa O và B nên A nằm giữa O và M. Khi đó, ta có: OA + MA = OM
Thay số: OA = 4 cm; MA = 1 cm ta được:
4 + 1 = OM
OM = 5cm
Vậy độ dài đoạn thẳng OM dài 5cm.
Bài 8.23 trang 57 Toán lớp 6 Tập 2: Trong hình vẽ dưới đây, em hãy liệt kê tất cả các bộ ba điểm thẳng hàng.

Lời giải:
Các bộ ba điểm thẳng hàng là:
A, C, N
A, C, B
A, N, B
C, N, B
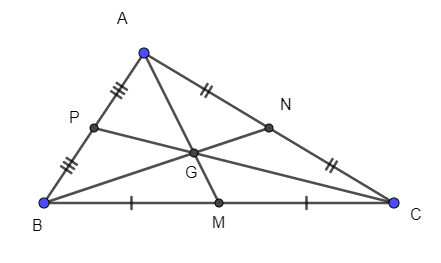
Bài 8.24 trang 57 Toán lớp 6 Tập 2: Em hãy vẽ 7 điểm trên một tờ giấy trắng sao cho có thể kẻ được 6 đường thẳng mà mỗi đường thẳng đều đi qua 3 trong 7 điểm đó.
Lời giải:
Gọi 7 điểm A, B, C, M, N, P và G như hình vẽ dưới:
Tham khảo lời giải bài tập Toán lớp 6 Kết nối tri thức với cuộc sống hay, chính xác nhất khác:

