Bài 7 trang 77 Toán 7 Tập 2 Cánh diều
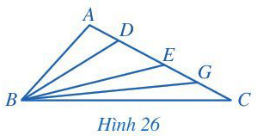
Cho tam giác ABC có góc A tù. Trên cạnh AC lần lượt lấy các điểm D, E, G sao cho D nằm giữa A và E; E nằm giữa D và G; G nằm giữa E và C (Hình 26).
Giải Toán 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác - Cánh diều
Bài 7 trang 77 Toán lớp 7 Tập 2: Cho tam giác ABC có góc A tù. Trên cạnh AC lần lượt lấy các điểm D, E, G sao cho D nằm giữa A và E; E nằm giữa D và G; G nằm giữa E và C (Hình 26).
Sắp xếp các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự độ dài tăng dần. Giải thích vì sao.
Lời giải:
Tam giác ABD có góc A tù nên góc A là góc lớn nhất trong tam giác ABD.
Do đó BD là cạnh lớn nhất trong tam giác ABD nên BA < BD (1).
là góc ngoài tại đỉnh D của tam giác ABD nên .
Do đó là góc tù.
Tam giác BDE có là góc tù nên là góc lớn nhất trong tam giác BDE.
Do đó BE là cạnh lớn nhất trong tam giác BDE nên BD < BE (2).
là góc ngoài tại đỉnh E của tam giác BDE nên .
Do đó là góc tù.
Tam giác BEG có là góc tù nên là góc lớn nhất trong tam giác BEG.
Do đó BG là cạnh lớn nhất trong tam giác BDE nên BE < BG (3).
là góc ngoài tại đỉnh G của tam giác BEG nên .
Do đó là góc tù.
Tam giác BGC có là góc tù nên là góc lớn nhất trong tam giác BGC.
Do đó BC là cạnh lớn nhất trong tam giác BGC nên BG < BC (4).
Từ (1), (2), (3) và (4) ta có BA < BD < BE < BG < BC.
Vậy các đoạn thẳng sắp xếp theo thứ tự tăng dần là: BA; BD; BE; BG; BC.
Lời giải bài tập Toán 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác hay, chi tiết khác:
Hoạt động 1 trang 74 Toán lớp 7 Tập 2: Quan sát tam giác ABC ở Hình 17 ....
Hoạt động 2 trang 75 Toán lớp 7 Tập 2: Quan sát tam giác ABC ở Hình 19 ....