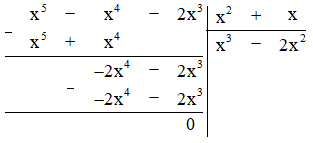Giải Toán 7 trang 68 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm giải Toán 7 trang 68 Tập 2 trong Bài tập cuối chương 6 Toán 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 68.

Giải Toán 7 trang 68 Tập 2 Cánh diều

Bài 1 trang 68 Toán lớp 7 Tập 2: Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.

a) -7x + 5.

b) 2 021x² - 2 022x + 2 023.

c) 2y³ - $\frac{3}{y+2}$ + 4.

d) -2t^m + 8t² + t - 1, với m là số tự nhiên lớn hơn 2.

Lời giải:

a) Biểu thức -7x + 5 là đa thức một biến x với bậc bằng 1.

b) Biểu thức 2 021x² - 2 022x + 2 023 là đa thức một biến x với bậc bằng 2.

c) Biểu thức 2y³ - $\frac{3}{y+2}$ + 4 không phải đa thức.

d) Biểu thức -2t^m + 8t² + t - 1 là đa thức một biến t với bậc bằng m, với m là số tự nhiên lớn hơn 2.

Bài 2 trang 68 Toán lớp 7 Tập 2: Tính giá trị của biểu thức:

a) A = -5a - b - 20 tại a = -4, b = 18;

b) B = -8xyz + 2xy + 16y tại x = -1, y = 3, z = -2;

c) C = -x^{2 021}y² + 9x^{2 021} tại x = -1, y = -3.

Lời giải:

a) Thay a = -4, b = 18 vào biểu thức trên ta được:

A = -5 . (-4) - 18 - 20 = 20 - 18 - 20 = -18.

Vậy A = -18 khi a = -4, b = 18.

b) Thay x = -1, y = 3, z = -2 vào biểu thức trên ta được:

B = -8 . (-1) . 3 . (-2) + 2 . (-1) . 3 + 16 . 3 = -48 + (-6) + 48 = -6.

Vậy B = -6 khi x = -1, y = 3, z = -2.

c) Thay x = -1, y = -3 vào biểu thức trên ta được:

C = - (-1)^{2 021} . (-3)² + 9 . (-1)^{2 021} = -(-1) . 9 + 9 . (-1) = 9 + (-9) = 0.

Vậy C = 9 khi x = -1, y = -3.

Bài 3 trang 68 Toán lớp 7 Tập 2: Viết đa thức trong mỗi trường hợp sau:

a) Đa thức bậc nhất có hệ số của biến bằng -2 và hệ số tự do bằng 6;

b) Đa thức bậc hai có hệ số tự do bằng 4;

c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0;

d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0.

Lời giải:

a) Đa thức bậc nhất có hệ số của biến bằng -2 và hệ số tự do bằng 6 là -2x + 6.

b) Đa thức bậc hai có hệ số tự do bằng 4 nên hệ số của lũy thừa bậc 2 của biến là một số khác 0 tùy ý, hệ số của lũy thừa bậc 1 của biến là một số tùy ý, hệ số tự do bằng 4.

Khi đó đa thức cần tìm có thể là x² + 4.

c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0 nên hệ số của lũy thừa bậc bốn của biến là một số khác 0 tùy ý, hệ số của lũy thừa bậc 3 của biến bằng 0, hệ số của lũy thừa bậc 2, bậc 1 của biến là một số tùy ý, hệ số tự do là một số tùy ý.

Khi đó đa thức cần tìm có thể là x⁴.

d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0 nên hệ số của lũy thừa bậc 6 của biến là một số khác 0 tùy ý, hệ số các lũy thừa bậc lẻ của biến bằng 0, hệ số các lũy thừa bậc chẵn còn lại của đa thức là một số tùy ý, hệ số tự do là một số tùy ý.

Khi đó đa thức cần tìm có thể là x⁶ + 1.

Bài 4 trang 68 Toán lớp 7 Tập 2: Kiểm tra xem trong các số -1, 0, 1, 2, số nào là nghiệm của mỗi đa thức sau:

a) 3x - 6;

b) x⁴ - 1;

c) 3x² - 4x;

d) x² + 9.

Lời giải:

a) Thay x = -1 vào đa thức trên ta có: 3 . (-1) - 6 = -3 - 6 = -9.

Thay x = 0 vào đa thức trên ta có: 3 . 0 - 6 = 0 - 6 = -6.

Thay x = 1 vào đa thức trên ta có: 3 . 1 - 6 = 3 - 6 = -3.

Thay x = 2 vào đa thức trên ta có: 3 . 2 - 6 = 6 - 6 = 0.

Do đó x = 2 là nghiệm của đa thức 3x - 6.

b) Thay x = -1 vào đa thức trên ta có: (-1)⁴ - 1 = 1 - 1 = 0.

Thay x = 0 vào đa thức trên ta có: 0⁴ - 1 = -1.

Thay x = 1 vào đa thức trên ta có: 1⁴ - 1 = 0.

Thay x = 2 vào đa thức trên ta có: 2⁴ - 1 = 16 - 1 = 15.

Do đó x = -1 và x = 1 là nghiệm của đa thức x⁴ - 1.

c) Thay x = -1 vào đa thức trên ta có: 3 . (-1)² - 4 . (-1)= 3 + 4 = 7.

Thay x = 0 vào đa thức trên ta có: 3 . 0² - 4 . 0 = 0.

Thay x = 1 vào đa thức trên ta có: 3 . 1² - 4 . 1 = 3 - 4 = -1.

Thay x = 2 vào đa thức trên ta có: 3 . 2² - 4 . 2 = 12 - 8 = 4.

Do đó x = 0 là nghiệm của đa thức 3x² - 4x.

d) Thay x = -1 vào đa thức trên ta có: (-1)² + 9 = 10.

Thay x = 0 vào đa thức trên ta có: 0² + 9 = 9.

Thay x = 1 vào đa thức trên ta có: 1² + 9 = 10.

Thay x = 2 vào đa thức trên ta có: 2² + 9 = 13.

Vậy trong 4 số trên, không có số nào là nghiệm của đa thức x² + 9.

Bài 5 trang 68 Toán lớp 7 Tập 2: Cho đa thức P(x) = -9x⁶ + 4x + 3x⁵ + 5x + 9x⁶ - 1.

a) Thu gọn đa thức P(x).

b) Tìm bậc của đa thức P(x).

c) Tính giá trị của đa thức P(x) tại x = -1; x = 0; x = 1.

Lời giải:

a) P(x) = -9x⁶ + 4x + 3x⁵ + 5x + 9x⁶ - 1

P(x) = (-9x⁶ + 9x⁶) + 3x⁵ + (4x + 5x) - 1

P(x) = 3x⁵ + 9x - 1.

b) Đa thức P(x) có bậc bằng 5.

c) Ta có:

P(-1) = 3 . (-1)⁵ + 9 . (-1) - 1 = 3 . (-1) + (-9) - 1 = -3 - 9 - 1 = -13.

P(0) = 3 . 0⁵ + 9 . 0 - 1 = -1.

P(1) = 3 . 1⁵ + 9 . 1 - 1 = 3 + 9 - 1 = 11.

Bài 6 trang 68 Toán lớp 7 Tập 2: Tính:

a) -2x² + 6x²;

b) 4x³ - 8x³;

c) 3x⁴(-6x²);

d) (-24x⁶) : (-4x³).

Lời giải:

a) -2x² + 6x² = (-2 + 6)x² = 4x2.

b) 4x³ - 8x³ = (4 - 8)x³ = -4x³.

c) 3x⁴(-6x²) = 3 . (-6) . x⁴ . x² = -18x⁶.

d) (-24x⁶) : (-4x³) = (-24 : -4) . (x⁶ : x³) = 6x³.

Bài 7 trang 68 Toán lớp 7 Tập 2: Tính:

a) (x² + 2x + 3) + (3x² - 5x + 1);

b) (4x³ - 2x² - 6) - (x³ - 7x² + x - 5);

c) -3x²(6x² - 8x + 1);

d) (4x² + 2x + 1)(2x - 1);

e) (x⁶ - 2x⁴ + x²) : (-2x²);

g) (x⁵ - x⁴ - 2x³) : (x² + x).

Lời giải:

a) (x² + 2x + 3) + (3x² - 5x + 1)

= x² + 2x + 3 + 3x² - 5x + 1

= (x² + 3x²) + (2x - 5x) + (3 + 1)

= 4x² - 3x + 4.

b) (4x³ - 2x² - 6) - (x³ - 7x² + x - 5)

= 4x³ - 2x² - 6 - x³ + 7x² - x + 5

= (4x³ - x³) + (-2x² + 7x²) - x + (-6 + 5)

= 3x³ + 5x² - x - 1.

c) -3x²(6x² - 8x + 1)

= -3x² . 6x² - (-3x²) . 8x + (-3x²) . 1

= -18x⁴ - (-24x³) - 3x²

= - 18x⁴ + 24x³ - 3x².

d) (4x² + 2x + 1)(2x - 1)

= 4x² . 2x - 4x² . 1 + 2x . 2x - 2x . 1 + 1 . 2x - 1.1

= 8x³ - 4x² + 4x² - 2x + 2x - 1

= 8x³ - 1.

e) (x⁶ - 2x⁴ + x²) : (-2x²)

= x⁶ : (-2x²) - 2x⁴ : (-2x²) + x² : (-2x²)

= $\frac{-1}{2}$x⁴ - (-x²) + $\left(\frac{-1}{2}\right)$

= $\frac{-1}{2}$x⁴ + x² - $\frac{1}{2}$.

g) Thực hiện phép tính ta được:

Vậy (x⁵ - x⁴ - 2x³) : (x² + x) = x³ - 2x².

Lời giải bài tập Toán lớp 7 Bài tập cuối chương 6 Cánh diều hay khác:

• Giải Toán 7 trang 69 Tập 2