Giải Toán 7 trang 73 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm giải Toán 7 trang 73 Tập 2 trong Bài 1: Tổng các góc của một tam giác Toán 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 73.

Giải Toán 7 trang 73 Tập 2 Cánh diều

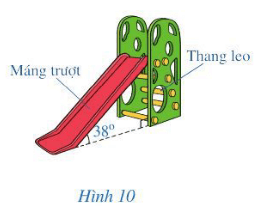
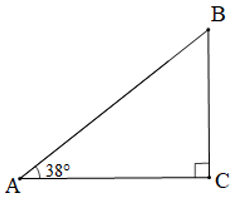
Bài 2 trang 73 Toán lớp 7 Tập 2: Hình 10 biểu diễn một chiếc cầu trượt gồm máng trượt và thang leo. Tính độ nghiêng của máng trượt so với phương thẳng đứng, biết rằng độ nghiêng của máng trượt so với mặt đất là 38°.

Lời giải:

Chiếc cầu trượt được minh họa và đặt tên các đỉnh như hình dưới đây:

Xét tam giác ABC vuông tại C:

$\hat{A}+\hat{B}=90°$(trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\hat{B}=90°-\hat{A}=90°-38°=52°$.

Vậy độ nghiêng của máng trượt so với phương thẳng đứng là 52°.

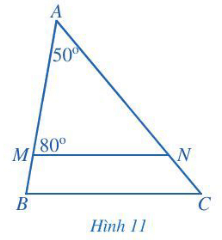
Bài 3 trang 73 Toán lớp 7 Tập 2: Trong Hình 11, MN // BC. Tính số đo góc C.

Lời giải:

Xét tam giác AMN: $\hat{A}+\hat{M}+\hat{N}=180°$.

Suy ra

$\hat{N}=180°-\hat{A}-\hat{M}=180°-50°-80°=50°$.

Do MN // BC nên $\hat{N}=\hat{C}$ (2 góc đồng vị).

Do đó $\hat{C}=50°$.

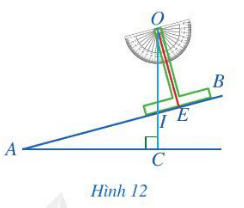
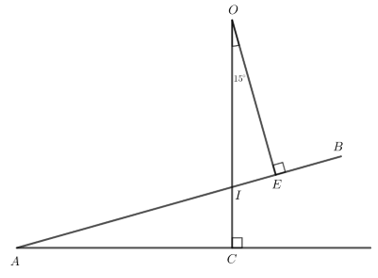
Bài 4 trang 73 Toán lớp 7 Tập 2: Hình 12 biểu diễn mặt cắt đứng của một đường lên dốc AB.

Để đo độ dốc của con đường biểu diễn bởi góc nhọn BAC tạo bởi đường thẳng AB với phương nằm ngang AC, người ta làm như sau:

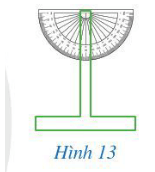
- Làm một thước chữ T như Hình 13;

- Đặt thước chữ T dọc theo cạnh AB như Hình 12, OE ⊥ AB

- Buộc một sợi dây vào chân O của thước chữ T và buộc một vật nặng vào đầu dây còn lại, sau đó thả vật nặng để sợi dây có phương thẳng đứng (trong xây dựng gọi là thả dây dọi);

- Tính góc BAC, biết rằng dây dọi OI tạo với trục OE của thước chữ T một góc 15°.

Lời giải:

Do OE ⊥ AB nên tam giác OIE vuông tại E.

Khi đó $\hat{O}+\widehat{OI\text{E}}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\hat{O}=90°-\widehat{OI\text{E}}$.

Xét $\Delta IC\text{A}$ vuông tại C có: $\widehat{IAC}+\widehat{AIC}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\widehat{IAC}=90°-\widehat{AIC}$.

Mà $\widehat{OI\text{E}}=\widehat{AIC}$ (2 góc đối đỉnh) nên $\hat{O}=\widehat{IAC}$ hay $\widehat{BAC}=15°$.

Vậy $\widehat{BAC}=15°$.

Lời giải bài tập Toán lớp 7 Bài 1: Tổng các góc của một tam giác Cánh diều hay khác:

• Giải Toán 7 trang 70 Tập 2

• Giải Toán 7 trang 72 Tập 2