Bài 2 trang 72 Toán 7 Tập 2 Chân trời sáng tạo
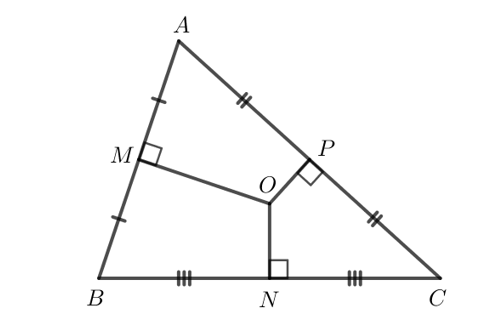
Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC và PO vuông góc với AC.
Giải Toán 7 Bài 6: Tính chất ba đường trung trực của tam giác - Chân trời sáng tạo
Bài 2 trang 72 Toán 7 Tập 2: Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC và PO vuông góc với AC.
Lời giải:
O là điểm cách đều 3 đỉnh của tam giác ABC nên O là giao điểm ba đường trung trực của tam giác ABC.
Khi đó do M, N, P lần lượt là trung điểm các cạnh AB, BC, CA nên MO AB, NO BC, PO AC.
Lời giải bài tập Toán 7 Bài 6: Tính chất ba đường trung trực của tam giác hay, chi tiết khác: