Bài 4.6 trang 67 Toán 7 Tập 1 - Kết nối tri thức

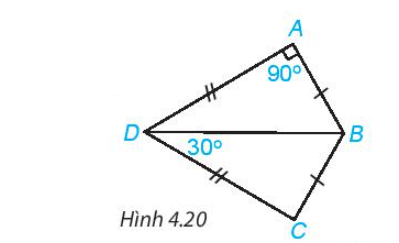
Cho Hình 4.20, biết AB = CB, AD = CD,  

Giải Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Bài 4.6 trang 67 Toán 7 Tập 1: Cho Hình 4.20, biết AB = CB, AD = CD, $\widehat{DAB}=90°,$ $\widehat{B\text{D}C}=30°.$

a) Chứng minh rằng $\Delta AB\text{D}=\Delta CB\text{D}.$

b) Tính $\widehat{ABC}.$

Lời giải:

a) Xét hai tam giác ABD và CBD có:

AB = BC (theo giả thiết).

AD = CD (theo giả thiết).

BD chung.

Vậy $\Delta AB\text{D}=\Delta CB\text{D}\left(c-c-c\right).$

b) Do $\Delta AB\text{D}=\Delta CB\text{D}$ nên $\widehat{A\text{D}B}=\widehat{C\text{D}B}$ (2 góc tương ứng).

Do đó $\widehat{A\text{D}B}=30°.$

Xét tam giác ABD vuông tại A có: $\widehat{AB\text{D}}+\widehat{A\text{D}B}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $\widehat{AB\text{D}}=90°-\widehat{A\text{D}B}=90°-30°=60°.$

Do $\Delta AB\text{D}=\Delta CB\text{D}$ nên $\widehat{ABD}=\widehat{CBD}$ (2 góc tương ứng).

Do đó $\widehat{CB\text{D}}=60°.$

Khi đó $\widehat{ABC}=\widehat{AB\text{D}}+\widehat{CB\text{D}}=60°+60°=120°.$

Vậy $\widehat{ABC}=120°.$

Lời giải bài tập Toán lớp 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Kết nối tri thức hay khác:

• Mở đầu trang 63 Toán 7 Tập 1: Ta nói hai đoạn thẳng bằng nhau nếu chúng có cùng độ dài, hai góc bằng nhau nếu chúng có cùng số đo góc. Vậy hai tam giác như thế nào thì được gọi là bằng nhau và làm thế nào để kiểm tra được hai tam giác đó bằng nhau? Trong bài này chúng ta sẽ trả lời câu hỏi đó. ....

• HĐ1 trang 63 Toán 7 Tập 1: Gấp đôi một tờ giấy rồi cắt như Hình 4.9. ....

• Câu hỏi trang 64 Toán 7 Tập 1: Biết hai tam giác trong Hình 4.11 bằng nhau, em hãy chỉ ra các cặp cạnh tương ứng, các cặp góc tương ứng và viết đúng kí hiệu bằng nhau của cặp tam giác đó. ....

• Luyện tập 1 trang 65 Toán 7 Tập 1: Cho tam giác ABC bằng tam giác DEF (H.4.13). Biết rằng BC = 4 cm, $\widehat{ABC}=40°,$ $\widehat{ACB}=60°.$ ....

• HĐ2 trang 65 Toán 7 Tập 1: Vẽ tam giác ABC có AB = 5 cm, AC = 4 cm, BC = 6 cm theo các bước sau: ....

• HĐ3 trang 66 Toán 7 Tập 1: Tương tự, vẽ thêm tam giác A'B'C' có A'B' = 5cm, A'C' = 4cm, B'C' = 6cm ....

• Câu hỏi trang 66 Toán 7 Tập 1: Trong Hình 4.15, những cặp tam giác nào bằng nhau? ....

• Luyện tập 2 trang 66 Toán 7 Tập 1: Cho Hình 4.17, biết AB = AD, BC = DC. ....

• Vận dụng trang 67 Toán 7 Tập 1: Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy như sau: ....

• Bài 4.4 trang 67 Toán 7 Tập 1: Cho hai tam giác ABC và DEF như Hình 4.18. ....

• Bài 4.5 trang 67 Toán 7 Tập 1: Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau. ....