Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.18).
Câu hỏi:
Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.18).
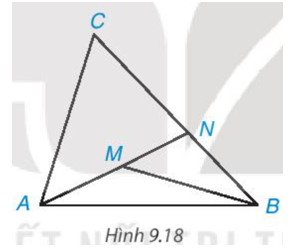
a) So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB.
Trả lời:
Trong tam giác ABD, theo bất đẳng thức tam giác ta có:
AD < AB + BD (1)
Trong tam giác ACD, theo bất đẳng thức tam giác ta có:
AD < AC + CD (2)
Từ (1) và (2) ta có:
AD + AD < AB + BD + AC + CD = AB + AC + (BD + CD)
Hay 2AD < AB + AC + BC
Suy ra AD < (AB + AC + BC).
Mặt khác chu vi tam giác ABC là AB + AC + BC.
Do đó AD nhỏ hơn nửa chu vi tam giác ABC.
Vậy AD nhỏ hơn nửa chu vi tam giác ABC.