Cho tam giác ABC có góc BAC là một góc tù. Lấy điểm D nằm giữa A và B; lấy điểm E
Câu hỏi:
Cho tam giác ABC có là một góc tù. Lấy điểm D nằm giữa A và B; lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
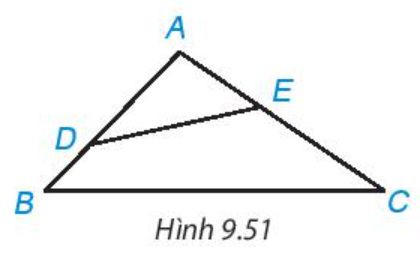
Trả lời:
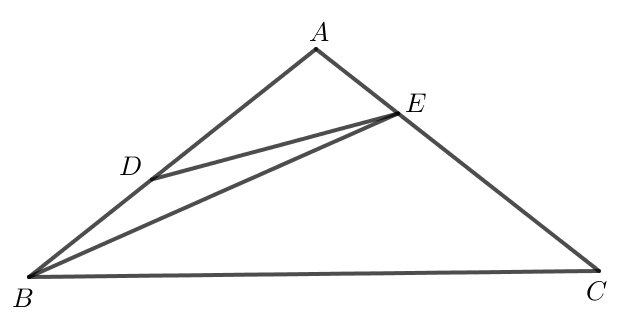
Xét tam giác ADE có là góc ngoài của đỉnh D nên
Mà là góc tù nên là góc tù.
Xét tam giác BDE có:
là góc tù nên là góc lớn nhất trong tam giác. Do đó, BE > DE (1)
Xét tam giác ABE có là góc ngoài của đỉnh E nên
Mà là góc tù nên là góc tù.
Xét tam giác BEC có:
là góc tù nên là góc lớn nhất trong tam giác. Do đó, BC > BE (2)
Từ (1) và (2) suy ra, BC > DE (điều phải chứng minh).

