Câu hỏi:
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:
a) AI < (AB + AC);
Trả lời:
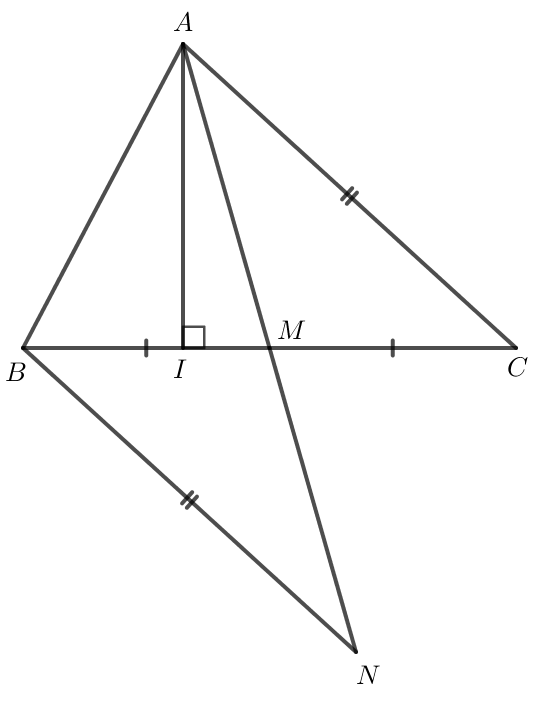
a)
vuông tại I nên AC là cạnh huyền.
Do đó AC > AI (1).
vuông tại I nên AB là cạnh huyền.
Do đó AB > AI (2).
Từ (1) và (2) ta có AB + AC > AI + Ai hay AB + AC > 2AI
Suy ra AI <
Câu 1:
Cho tam giác ABC có là một góc tù. Lấy điểm D nằm giữa A và B; lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
Câu 2:
Cho tam giác ABC (AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA (H.9.52).
a) So sánh và .
Câu 5:
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD = 2DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A.
Gợi ý. D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là đường trung tuyến.
Câu 6:
Một sợi dây thép dài 1,2 m. Cần đánh dấu trên sợi dây thép đó hai điểm để khi uốn gập nó lại tại hai điểm đó sẽ tạo thành tam giác cân có một cạnh dài 30 cm (H.9.54). Em hãy mô tả các cách đánh dấu hai điểm trên sợi dây thép.
