Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC

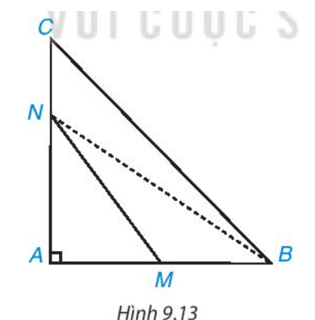
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC (M, N không phải là đỉnh của tam giác) (H.9.13). Chứng minh rằng MN < BC.

(Gợi ý. So sánh MN với NB, NB với BC).

Ta có $\widehat{NMB}$ là góc ngoài tại đỉnh M của tam giác AMN nên $\widehat{NMB}=\widehat{ANM}+\widehat{NAM}>\widehat{NAM}$ 

Do đó $\widehat{NMB}$ là góc tù.

$\Delta NMB$ có $\widehat{NMB}$ là góc tù nên $\Delta NMB$ là tam giác tù.

Do đó cạnh NB đối diện với $\widehat{NMB}$là cạnh lớn nhất trong $\Delta NMB$.

Khi đó MN < NB (1).

$\widehat{CNB}$ là góc ngoài tại đỉnh N của $\Delta ANB$ nên $\widehat{CNB}=\widehat{NBA}+\widehat{BAN}>\widehat{BAN}={90}^o$.

Do đó $\widehat{CNB}$ là góc tù.

$\Delta CNB$ có $\widehat{CNB}$ là góc tù nên $\Delta CNB$ là tam giác tù.

Do đó cạnh BC đối diện với $\widehat{CNB}$ là cạnh lớn nhất trong $\Delta CNB$.

Khi đó NB < BC (2).

Từ (1) và (2) ta có MN < NB < BC.

Vậy MN < BC.