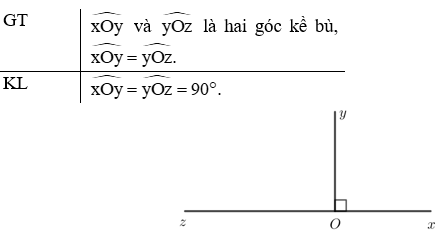Giải Toán 7 trang 57 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 57 Tập 1 trong Bài 11: Định lí và chứng minh định lí Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 57.

Giải Toán 7 trang 57 Tập 1 Kết nối tri thức

Luyện tập 2 trang 57 Toán 7 Tập 1: Em hãy chứng minh định lí: “Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”.

Lời giải:

Chứng minh:

Do $\widehat{xOy}$ và $\widehat{y\text{O}z}$ là hai góc kề bù nên $\widehat{xOy}+\widehat{y\text{O}z}=180°.$

Mà $\widehat{xOy}=\widehat{y\text{O}z}$ nên $\widehat{xOy}+\widehat{y\text{O}z}=2\widehat{xOy}=180°$

Do đó $\widehat{xOy}=\widehat{y\text{O}z}=90°.$

Vậy hai góc kề bù bằng nhau thì mỗi góc là một góc vuông.

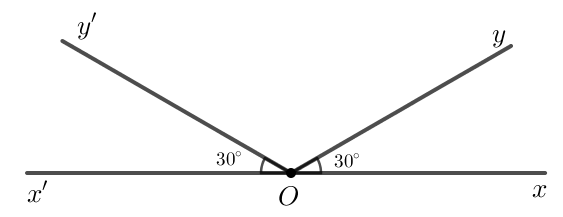
Tranh luận trang 57 Toán 7 Tập 1: Hình tròn: Hai góc đối đỉnh thì chắc chắn bằng nhau rồi. Liệu hai góc bằng nhau thì có đối đỉnh không nhỉ?

Hình vuông: Tớ nghĩ đó là điều không đúng! Nhưng làm thế nào để khẳng định điều đó không đúng nhỉ?

Em có ý kiến gì về hai ý kiến trên?

Lời giải:

Hai góc bằng nhau thì chưa chắc đối đỉnh.

Hình vẽ bên dưới ta có $\widehat{xOy}=\widehat{x^{\text{'}}O{y}^{\text{'}}}=30°$ nhưng hai góc này không đối đỉnh.

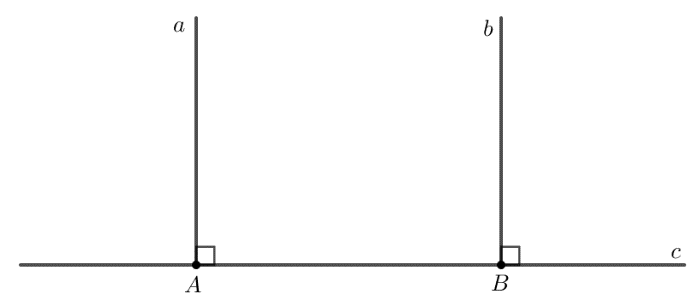
Bài 3.24 trang 57 Toán 7 Tập 1: Có thể coi định lí “ Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song không? Suy ra như thế nào?

Lời giải:

Định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.

Trong hình vẽ trên, ta có hai đường thẳng a và b cùng vuông góc với đường thẳng c.

Giao điểm của hai đường thẳng a và b với đường thẳng c lần lượt là A và B.

Do đường thẳng a và đường thẳng b vuông góc với đường thẳng c nên $\widehat{aAc}=\widehat{bBc}=90°.$

Mà hai góc này ở vị trí đồng vị nên a song song với b.

Vậy ta có điều phải chứng minh.

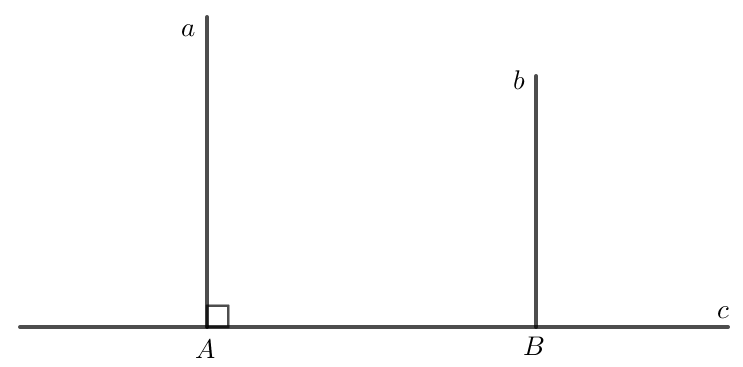
Bài 3.25 trang 57 Toán 7 Tập 1: Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó ta đã sử dụng những điều đúng đã biết nào?

Lời giải:

Trong hình vẽ trên, ta có hai đường thẳng a và b song song với nhau.

Đường thẳng c vuông góc với đường thẳng a.

Giao điểm của hai đường thẳng a và b với đường thẳng c lần lượt là A và B.

Do đường thẳng a vuông góc với đường thẳng c nên $\widehat{aAc}=90°.$

Do đường thẳng a song song với đường thẳng b nên $\widehat{aAc}=\widehat{bBc}$ (hai góc đồng vị)

Do đó $\widehat{bBc}=90°.$

Vậy đường thẳng b vuông góc với đường thẳng c.

Trong chứng minh này, chúng ta sử dụng các kiến thức về số đo của góc vuông, các góc tạo bởi hai đường thẳng cắt nhau, tính chất hai đường thẳng song song.

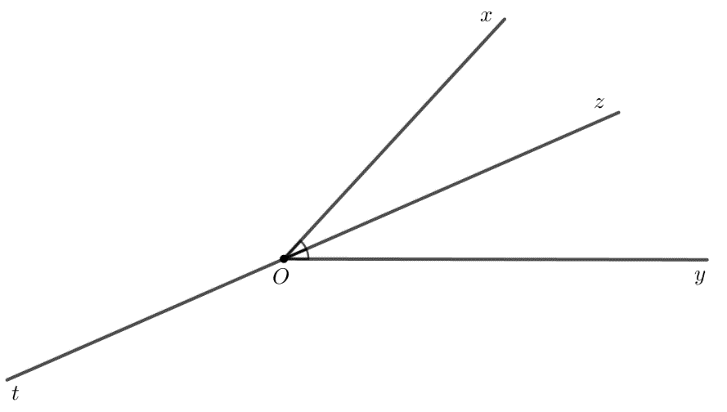
Bài 3.26 trang 57 Toán 7 Tập 1: Cho góc xOy không phải góc bẹt. Khẳng định nào sau đây là đúng?

(1) Nếu Ot là tia phân giác của góc xOy thì $\widehat{xOt}=\widehat{tOy}.$

(2) Nếu tia Ot thỏa mãn $\widehat{xOt}=\widehat{tOy}$ thì Ot là tia phân giác của góc xOy.

Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng.

(Gợi ý: Xét tia đối của một tia phân giác).

Lời giải:

Khẳng định (1) đúng dựa vào tính chất tia phân giác của góc.

Khẳng định (2) sai, ta có ví dụ như sau:

Trong hình vẽ trên, Oz là tia phân giác của góc xOy, Ot là tia đối của Oz.

Do Oz là tia phân giác của góc xOy nên $\widehat{xOz}=\widehat{zOy}$ (tính chất tia phân giác của góc).

Mà $\widehat{xOt}+\widehat{xOz}=180°,\widehat{y\text{O}t}+\widehat{zOy}=180°$ (hai góc kề bù) nên $\widehat{xOt}=\widehat{tOy}.$

Ta thấy $\widehat{xOt}=\widehat{tOy}$ mà Ot không phải tia phân giác của góc xOy nên khẳng định (2) sai.

Lời giải bài tập Toán lớp 7 Bài 11: Định lí và chứng minh định lí Kết nối tri thức hay khác:

• Giải Toán 7 trang 56 Tập 1