Giải Toán 7 trang 67 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 67 Tập 1 trong Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 67.

Giải Toán 7 trang 67 Tập 1 Kết nối tri thức

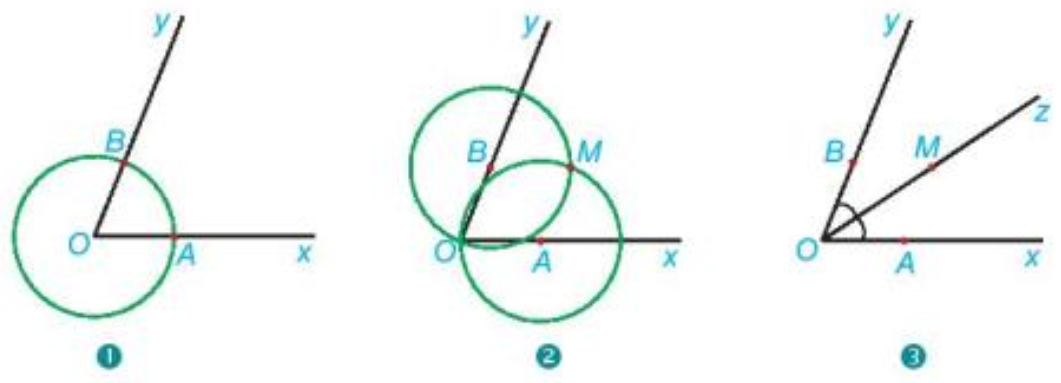
Vận dụng trang 67 Toán 7 Tập 1: Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy như sau:

(1) Vẽ đường tròn tâm O cắt Ox, Oy lần lượt tại A và B.

(2) Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.

(3) Vẽ tia Oz đi qua M.

Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.

Lời giải:

Do A và B thuộc đường tròn tâm O nên AO = BO.

Do M thuộc đường tròn tâm B bán kính BO nên BO = BM.

Do M thuộc đường tròn tâm A bán kính AO nên AO = AM.

Mà AO = BO nên AM = BM.

Xét hai tam giác OBM và OAM có:

BO = AO (chứng minh trên).

BM = AM (chứng minh trên).

OM chung.

Do đó $\Delta OBM=\Delta OAM\left(c-c-c\right).$

Do đó $\widehat{BOM}=\widehat{AOM}$ (2 góc tương ứng).

Mà OM nằm giữa hai tia OA và OB nên OM là tia phân giác của $\widehat{AOB}$ hay OM là tia phân giác của $\widehat{xOy}.$

Vậy OM là tia phân giác của $\widehat{xOy}.$

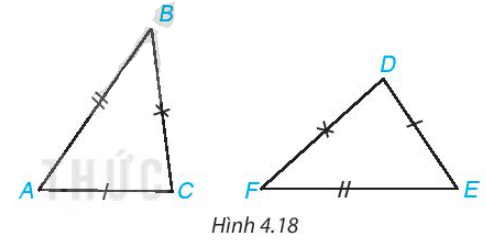
Bài 4.4 trang 67 Toán 7 Tập 1: Cho hai tam giác ABC và DEF như Hình 4.18.

Trong các khẳng định sau, khẳng định nào đúng?

(1) $\Delta ABC=\Delta DEF;$

(2) $\Delta ACB=\Delta EDF;$

(3) $\Delta BAC=\Delta DFE;$

(4) $\Delta CAB=\Delta DEF.$

Lời giải:

Quan sát hình, ta thấy AB = EF, BC = FD, CA = DE.

Khi đó:

$\Delta ABC=\Delta EFD$ nên khẳng định (1) sai.

$\Delta ACB=\Delta E\text{D}F$ nên khẳng định (2) đúng.

$\Delta BAC=\Delta F\text{ED}$ nên khẳng định (3) sai.

$\Delta CAB=\Delta DEF$ nên khẳng định (4) đúng.

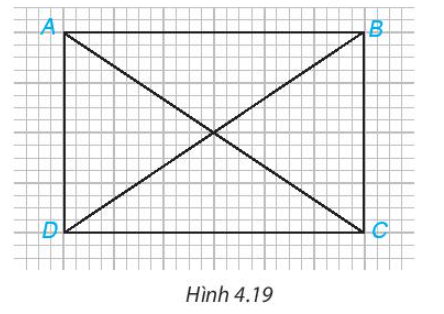
Bài 4.5 trang 67 Toán 7 Tập 1: Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.

Lời giải:

Xét hai tam giác ABD và CDB có:

AB = CD (cùng có độ dài bằng 6 ô vuông).

AD = BC (cùng có độ dài bằng 4 ô vuông).

BD chung.

Do đó $\Delta AB\text{D}=\Delta C\text{D}B\left(c-c-c\right).$

Xét hai tam giác ACD và CAB có:

AD = BC (cùng có độ dài bằng 4 ô vuông).

CD = AB (cùng có độ dài bằng 6 ô vuông).

AC chung.

Do đó $\Delta AC\text{D}=\Delta CAB\left(c-c-c\right).$

Vậy hai cặp tam giác bằng nhau là: ∆ABD = ∆CDB, ∆ACD = ∆CAB

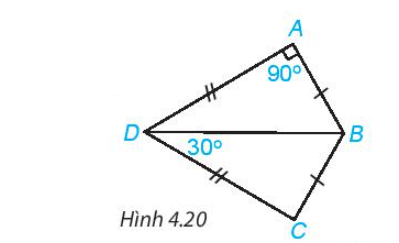
Bài 4.6 trang 67 Toán 7 Tập 1: Cho Hình 4.20, biết AB = CB, AD = CD, $\widehat{DAB}=90°,$ $\widehat{B\text{D}C}=30°.$

a) Chứng minh rằng $\Delta AB\text{D}=\Delta CB\text{D}.$

b) Tính $\widehat{ABC}.$

Lời giải:

a) Xét hai tam giác ABD và CBD có:

AB = BC (theo giả thiết).

AD = CD (theo giả thiết).

BD chung.

Vậy $\Delta AB\text{D}=\Delta CB\text{D}\left(c-c-c\right).$

b) Do $\Delta AB\text{D}=\Delta CB\text{D}$ nên $\widehat{A\text{D}B}=\widehat{C\text{D}B}$ (2 góc tương ứng).

Do đó $\widehat{A\text{D}B}=30°.$

Xét tam giác ABD vuông tại A có: $\widehat{AB\text{D}}+\widehat{A\text{D}B}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $\widehat{AB\text{D}}=90°-\widehat{A\text{D}B}=90°-30°=60°.$

Do $\Delta AB\text{D}=\Delta CB\text{D}$ nên $\widehat{ABD}=\widehat{CBD}$ (2 góc tương ứng).

Do đó $\widehat{CB\text{D}}=60°.$

Khi đó $\widehat{ABC}=\widehat{AB\text{D}}+\widehat{CB\text{D}}=60°+60°=120°.$

Vậy $\widehat{ABC}=120°.$

Lời giải bài tập Toán lớp 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Kết nối tri thức hay khác:

• Giải Toán 7 trang 63 Tập 1
• Giải Toán 7 trang 64 Tập 1
• Giải Toán 7 trang 65 Tập 1
• Giải Toán 7 trang 66 Tập 1