Giải Toán 7 trang 69 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 69 Tập 1 trong Luyện tập chung trang 68 Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 69.

Giải Toán 7 trang 69 Tập 1 Kết nối tri thức

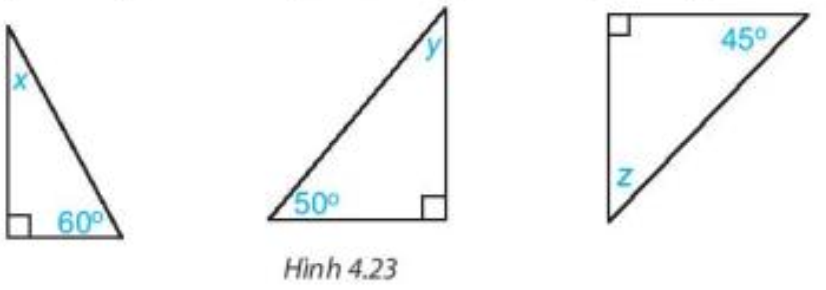
Bài 4.7 trang 69 Toán 7 Tập 1: Các số đo x, y, z trong mỗi tam giác vuông dưới đây bằng bao nhiêu độ?

Lời giải:

Xét tam giác vuông trong hình đầu tiên ta có: $x+60°=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $x=90°-60°=30°.$

Xét tam giác vuông trong hình thứ hai ta có: $y+50°=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $y=90°-50°=40°.$

Xét tam giác vuông trong hình thứ ba ta có: $z+45°=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $z=90°-45°=45°.$

Vậy $x=30°,y=40°,z=45°.$

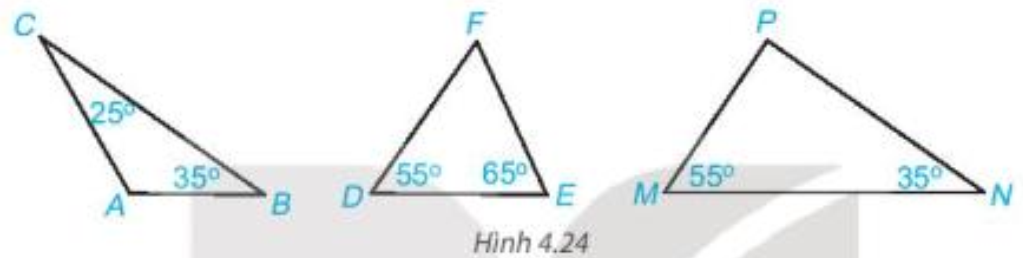
Bài 4.8 trang 69 Toán 7 Tập 1: Tính số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.

Lời giải:

Xét tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}=180°.$

Do đó $\widehat{A}=180°-\widehat{B}-\widehat{C}=180°-35°-25°=120°.$

Tam giác ABC không có góc vuông nên tam giác ABC không phải tam giác vuông.

Xét tam giác DEF có $\widehat{D}+\widehat{E}+\widehat{E}=180°.$

Do đó $\widehat{F}=180°-\widehat{D}-\widehat{E}=180°-55°-65°=60°.$

Tam giác DEF không có góc vuông nên tam giác DEF không phải tam giác vuông.

Xét tam giác MNP có $\widehat{M}+\widehat{N}+\widehat{P}=180°.$

Do đó $\widehat{P}=180°-\widehat{M}-\widehat{N}=180°-55°-35°=90°.$

Do đó góc P là góc vuông.

Tam giác MNP có một góc vuông nên tam giác MNP là tam giác vuông.

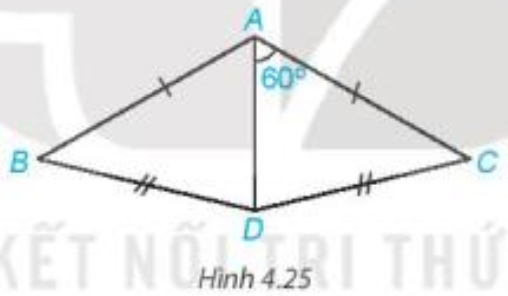
Bài 4.9 trang 69 Toán 7 Tập 1: Cho Hình 4.25, biết $\widehat{DAC}=60°,$ AB = AC, DB = DC. Hãy tính $\widehat{DAB}.$

Lời giải:

Xét hai tam giác ADB và ADC có:

AB = AC (theo giả thiết).

BD = CD (theo giả thiết).

AD chung.

Do đó $\Delta A\text{D}B=\Delta A\text{D}C\left(c-c-c\right).$

Do đó $\widehat{DAB}=\widehat{DAC}$ (2 góc tương ứng).

Vậy $\widehat{DAB}=60°.$

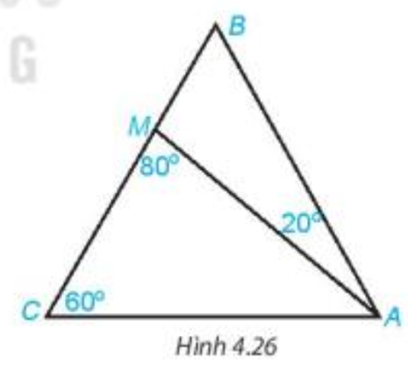
Bài 4.10 trang 69 Toán 7 Tập 1: Cho tam giác ABC có $\widehat{BCA}=60°$ và điểm M nằm trên cạnh BC sao cho $\widehat{BAM}=20°,\widehat{AMC}=80°$ (H.4.26). Tính số đo các góc AMB, ABC, BAC.

Lời giải:

 

Xét tam giác AMC có:

$\widehat{AMC}+\widehat{ACM}+\widehat{MAC}=180°.$

Do đó $\widehat{MAC}=180°-\widehat{AMC}-\widehat{ACM}=180°-80°-60°=40°.$

$\widehat{AMB}$ là góc ngoài tại đỉnh M của tam giác AMC nên

$\widehat{AMB}=\widehat{ACM}+\widehat{MAC}=60°+40°=100°.$

Xét tam giác AMB có $\widehat{AMB}+\widehat{MAB}+\widehat{ABM}=180°.$

Do đó $\widehat{ABM}=180°-\widehat{AMB}-\widehat{MAB}=180°-100°-20°=60°.$

hay $\widehat{ABC}=60°.$

Ta có $\widehat{BAC}=\widehat{MAB}+\widehat{MAC}=20°+40°=60°.$

Vậy $\widehat{AMB}=100°,\widehat{ABC}=60°,\widehat{BAC}=60°.$

Bài 4.11 trang 69 Toán 7 Tập 1: Cho $\Delta ABC=\Delta DEF.$ Biết rằng $\widehat{A}=60°,\widehat{E}=80°,$ tính số đo các góc B, C, D, F.

Lời giải:

Do $\Delta ABC=\Delta DEF$ nên ta có các cặp góc tương ứng bằng nhau:

$\widehat{A}=\widehat{D}=60°,\widehat{B}=\widehat{E}=80°,\widehat{C}=\widehat{F}.$

Xét tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}=180°.$

Do đó $\widehat{C}=180°-\widehat{A}-\widehat{B}=180°-60°-80°=40°.$

Mà $\widehat{C}=\widehat{F}$ nên $\widehat{F}=40°.$

Vậy $\widehat{B}=80°,\widehat{D}=60°,\widehat{C}=\widehat{F}=40°.$