Giải Toán 7 trang 74 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 74 Tập 1 trong Luyện tập chung trang 74 Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 74.

Giải Toán 7 trang 74 Tập 1 Kết nối tri thức

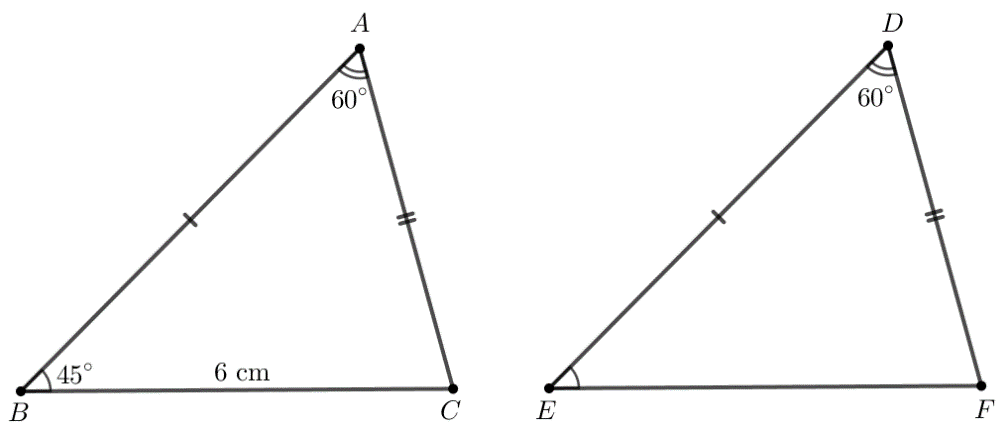
Bài 4.16 trang 74 Toán 7 Tập 1: Cho hai tam giác ABC và DEF thỏa mãn AB = DE, AC = DF,  $\widehat{BAC}=\widehat{E\text{D}F}=60°,$ BC = 6 cm, $\widehat{ABC}=45°.$ Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.

Lời giải:

Xét hai tam giác ABC và DEF có:

AB = DE (theo giả thiết).

$\widehat{BAC}=\widehat{E\text{D}F}$ (theo giả thiết).

AC = DF (theo giả thiết).

Vậy $\Delta ABC=\Delta D\text{EF}$ (c – g – c).

Do đó BC = EF = 6 cm (2 cạnh tương ứng), $\widehat{ACB}=\widehat{DF\text{E}}$ (2 góc tương ứng),

$\widehat{ABC}=\widehat{\text{DEF}}=45°$ (2 góc tương ứng).

Xét tam giác ABC có $\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180°.$

Do đó

 $$\begin{gathered} \widehat{ACB}=180°-\widehat{ABC}-\widehat{BAC} \\ =180°-45°-60°=75°. \end{gathered}$$

Do đó $\widehat{DF\text{E}}=75°.$

Vậy EF = 6 cm, $\widehat{ACB}=\widehat{EFD}=75°,\widehat{\text{DEF}}=45°.$

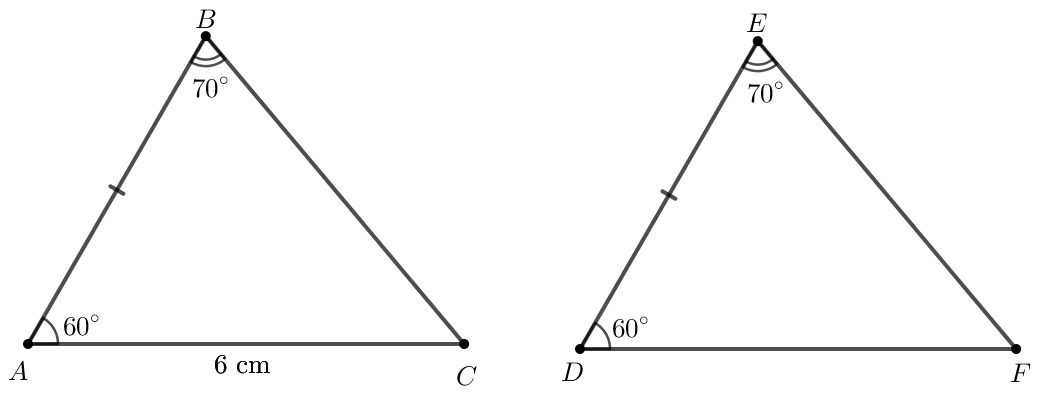
Bài 4.17 trang 74 Toán 7 Tập 1: Cho hai tam giác ABC và DEF thỏa mãn AB = DE, $\widehat{ABC}=\widehat{DEF}=70°,\widehat{BAC}=\widehat{EDF}=60°,$ AC = 6 cm. Tính độ dài cạnh DF.

Lời giải:

Xét hai tam giác ABC và DEF có:

$\widehat{ABC}=\widehat{DEF}$ (theo giả thiết).

AB = DE (theo giả thiết).

$\widehat{BAC}=\widehat{EDF}$ (theo giả thiết).

Vậy $\Delta ABC=\Delta D\text{EF}$ (g – c – g).

Do đó AC = DF = 6 cm (2 cạnh tương ứng).

Vậy DF = 6 cm.

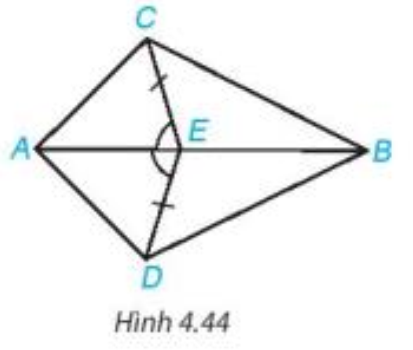
Bài 4.18 trang 74 Toán 7 Tập 1: Cho Hình 4.44, biết EC = ED và $\widehat{A\text{E}C}=\widehat{A\text{ED}}.$ Chứng minh rằng:

a) $\Delta A\text{E}C=\Delta A\text{ED};$

b) $\Delta ABC=\Delta AB\text{D}.$

Lời giải:

a) Xét hai tam giác AEC và AED có:

CE = DE (theo giả thiết).

$\widehat{CEA}=\widehat{DE\text{A}}$ (theo giả thiết).

AE chung

Vậy $\Delta A\text{E}C=\Delta A\text{ED}$ (c – g – c).

b) Do $\Delta A\text{E}C=\Delta A\text{ED}$ nên AC = AD (2 cạnh tương ứng) và $\widehat{CA\text{E}}=\widehat{DA\text{E}}$ (2 góc tương ứng).

Do $\widehat{CA\text{E}}=\widehat{DA\text{E}}$ nên $\widehat{CAB}=\widehat{DAB}.$

Xét hai tam giác ABC và ABD có:

AC = AD (chứng minh trên).

$\widehat{CAB}=\widehat{DAB}$ (chứng minh trên).

AB chung.

Vậy $\Delta ABC=\Delta AB\text{D}$ (c – g – c).

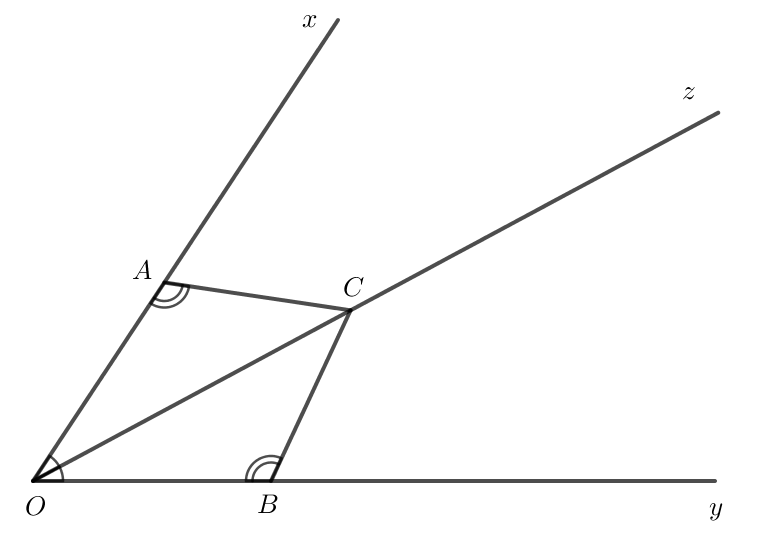
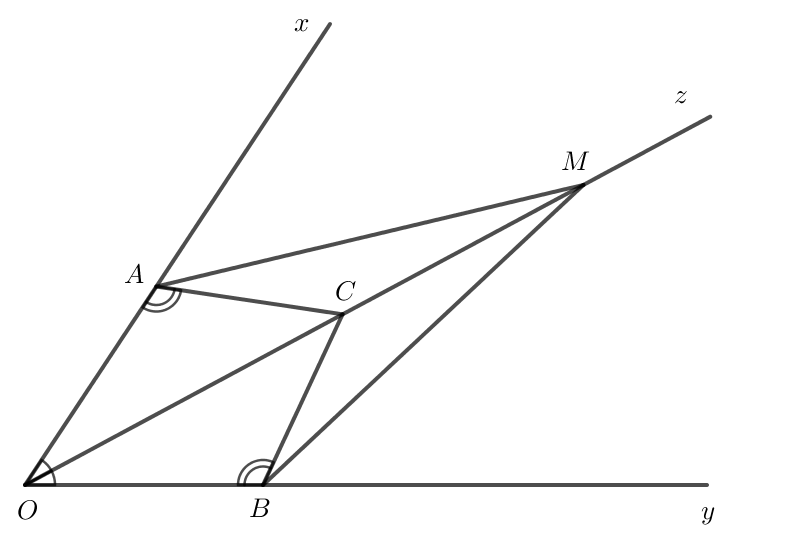
Bài 4.19 trang 74 Toán 7 Tập 1: Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho $\widehat{CAO}=\widehat{CBO}.$

a) Chứng minh rằng $\Delta OAC=\Delta OBC.$

b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng $\Delta MAC=\Delta MBC.$

Lời giải:

a)

Do Oz là tia phân giác của góc xOy nên $\widehat{AOC}=\widehat{BOC}.$

Xét tam giác OAC có $\widehat{AOC}+\widehat{CAO}+\widehat{AC\text{O}}=180°.$

Do đó $\widehat{ACO}=180°-\widehat{AOC}-\widehat{CAO}$ (1).

Xét tam giác OBC có $\widehat{BOC}+\widehat{CBO}+\widehat{BC\text{O}}=180°.$

Do đó $\widehat{BCO}=180°-\widehat{BOC}-\widehat{CBO}$ (2).

Mà $\widehat{AOC}=\widehat{BOC}$ và $\widehat{CAO}=\widehat{CBO}$ nên từ (1) và (2) ta có $\widehat{AC\text{O}}=\widehat{BCO}.$

Xét hai tam giác OAC và OBC có:

$\widehat{AOC}=\widehat{BOC}$ (chứng minh trên).

OC chung.

$\widehat{AC\text{O}}=\widehat{BCO}$ (chứng minh trên).

Vậy $\Delta OAC=\Delta OBC$ (g – c – g).

b)

Ta có $\widehat{ACM}$ là góc ngoài tại đỉnh C của tam giác OAC nên $\widehat{ACM}=\widehat{AOC}+\widehat{CAO}.$

$\widehat{BCM}$ là góc ngoài tại đỉnh C của tam giác OBC nên $\widehat{BCM}=\widehat{BOC}+\widehat{CBO}.$

Mà $\widehat{AOC}=\widehat{BOC}$ và $\widehat{CAO}=\widehat{CBO}$ nên $\widehat{ACM}=\widehat{BCM}.$

Do $\Delta OAC=\Delta OBC$ nên AC = BC (2 cạnh tương ứng).

Xét hai tam giác MAC và MBC có:

AC = BC (chứng minh trên).

$\widehat{ACM}=\widehat{BCM}$ (chứng minh trên).

MC chung.

Vậy $\Delta MAC=\Delta MBC$ (c – g – c).