Giải Toán 7 trang 79 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 79 Tập 1 trong Bài 15: Các trường hợp bằng nhau của tam giác vuông Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 79.

Giải Toán 7 trang 79 Tập 1 Kết nối tri thức

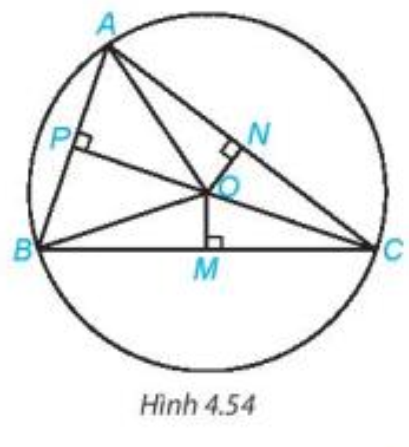
Luyện tập 3 trang 79 Toán 7 Tập 1: Cho ba điểm A, B, C nằm trên đường tròn tâm O và các điểm M, N, P như Hình 4.54. Hãy chỉ ra ba cặp tam giác vuông bằng nhau trong hình.

Lời giải:

Do A, B, C nằm trên đường tròn tâm O nên OA = OB = OC.

Xét hai tam giác ONA vuông tại N và ONC vuông tại N có:

OA = OC (chứng minh trên).

ON chung.

Do đó $\Delta ON\text{A}=\Delta ONC$ (cạnh huyền – cạnh góc vuông).

Xét hai tam giác OMB vuông tại M và OMC vuông tại M có:

OB = OC (chứng minh trên).

OM chung.

Do đó $\Delta OMB=\Delta OMC$ (cạnh huyền – cạnh góc vuông).

Xét hai tam giác OPA vuông tại P và OPB vuông tại P có:

OA = OB (chứng minh trên).

OP chung.

Do đó $\Delta OPA=\Delta OPB$ (cạnh huyền – cạnh góc vuông).

Vậy $\Delta ON\text{A}=\Delta ONC,\Delta OMB=\Delta OMC,\Delta OPA=\Delta OPB.$

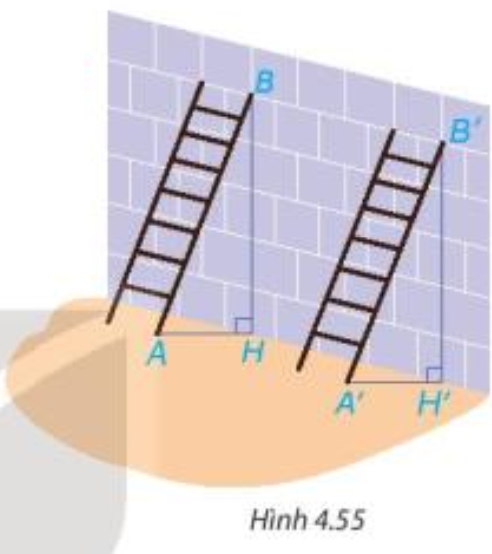
Thử thách nhỏ trang 79 Toán 7 Tập 1: Có hai chiếc thang dài như nhau được dựa vào một bức tường với cùng độ cao $BH=B^{\text{'}}{H}^{\text{'}}$ như Hình 4.55. Các góc BAH và $B^{\text{'}}{A}^{\text{'}}{H}^{\text{'}}$ có bằng nhau không? Vì sao?

Lời giải:

Xét hai tam giác BAH vuông tại H và $B^{\text{'}}{H}^{\text{'}}{A}^{\text{'}}$ vuông tại $H^{\text{'}}$ có:

$BA=B^{\text{'}}{A}^{\text{'}}$ (theo giả thiết).

$BH=B^{\text{'}}{H}^{\text{'}}$ (theo giả thiết).

Do đó $\Delta BAH=\Delta B^{\text{'}}{A}^{\text{'}}{H}^{\text{'}}$ (cạnh huyền – cạnh góc vuông).

Vậy $\widehat{BAH}=\widehat{B^{\text{'}}{A}^{\text{'}}{H}^{\text{'}}}$ (2 góc tương ứng).

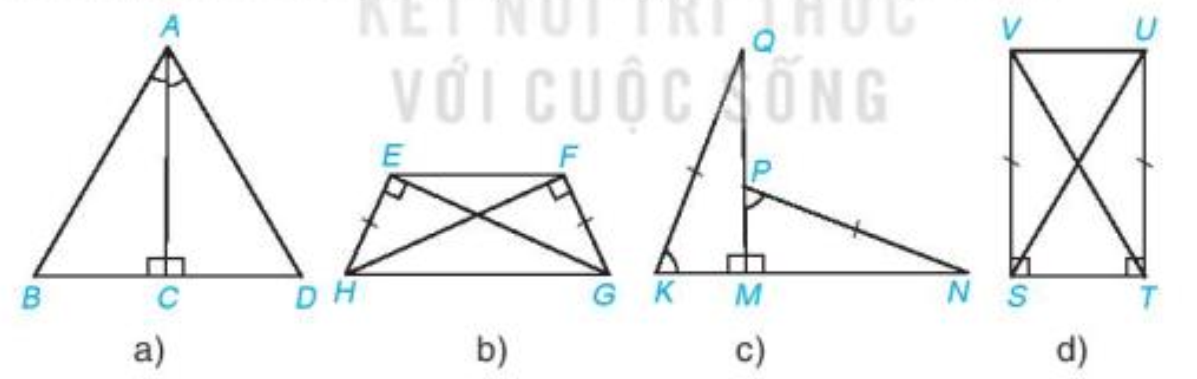
Bài 4.20 trang 79 Toán 7 Tập 1: Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?

Lời giải:

a) Xét hai tam giác ACB vuông tại C và ACD vuông tại C có:

$\widehat{CAB}=\widehat{CA\text{D}}$ (theo giả thiết).

AC chung.

Vậy $\Delta ACB=\Delta AC\text{D}$ (góc nhọn – cạnh góc vuông).

b) Xét hai tam giác EGH vuông tại E và FHG vuông tại F có:

EH = FG (theo giả thiết).

HG chung.

Vậy $\Delta EGH=\Delta FHG$ (cạnh huyền – cạnh góc vuông).

c) Xét hai tam giác QMK vuông tại M và NMP vuông tại M có:

QK = NP (theo giả thiết).

$\widehat{QKM}=\widehat{NPM}$ (theo giả thiết).

Vậy $\Delta QMK=\Delta NMP$ (cạnh huyền – góc nhọn).

d) Xét hai tam giác VST vuông tại S và UTS vuông tại T có:

VS = UT (theo giả thiết).

ST chung.

Vậy $\Delta V\text{S}T=\Delta UTS$ (2 cạnh góc vuông).

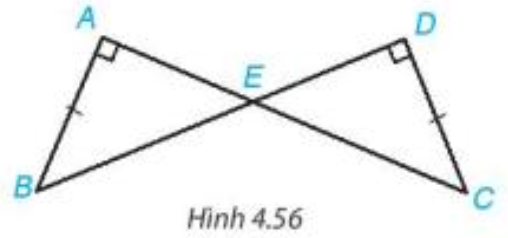
Bài 4.21 trang 79 Toán 7 Tập 1: Cho Hình 4.56, biết AB = CD, $\widehat{BAC}=\widehat{B\text{D}C}=90°.$ Chứng minh rằng $\Delta ABE=\Delta DCE.$

Lời giải:

Xét tam giác ABE có $\widehat{BAE}+\widehat{ABE}+\widehat{AEB}=180°.$

Do đó $\widehat{ABE}=180°-\widehat{BAE}-\widehat{AEB}$ (1).

Xét tam giác DCE có $\widehat{CDE}+\widehat{DCE}+\widehat{\text{D}EC}=180°.$

Do đó $\widehat{DCE}=180°-\widehat{CDE}-\widehat{DEC}$ (2).

Mà $\widehat{BA\text{E}}=\widehat{C\text{D}E}=90°,\widehat{A\text{E}B}=\widehat{DEC}$ (2 góc đối đỉnh) nên từ (1) và (2) có $\widehat{ABE}=\widehat{DCE}.$

Xét hai tam giác ABE vuông tại A và DCE vuông tại E có:

$\widehat{ABE}=\widehat{DCE}$ (chứng minh trên).

AB = DC (theo giả thiết).

Vậy $\Delta ABE=\Delta DCE$ (góc nhọn – cạnh góc vuông).

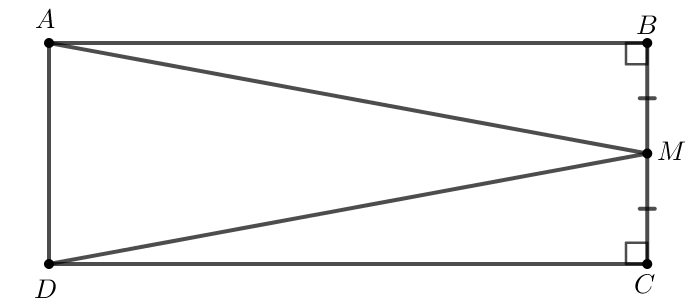
Bài 4.22 trang 79 Toán 7 Tập 1: Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.

Chứng minh rằng $\Delta ABM=\Delta DCM.$

Lời giải:

Do ABCD là hình chữ nhật nên $\widehat{ABC}=\widehat{BC\text{D}}=90°,AB=C\text{D}.$

Hay $\widehat{ABM}=\widehat{DCM}=90°.$

Do đó tam giác ABM vuông tại B, tam giác DCM vuông tại C.

Do M là trung điểm của cạnh BC nên MB = MC.

Xét hai tam giác ABM vuông tại B và DCM vuông tại C có:

AB = CD (chứng minh trên).

MB = MC (chứng minh trên).

Vậy $\Delta ABM=\Delta DCM$ (2 cạnh góc vuông).

Lời giải bài tập Toán lớp 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông Kết nối tri thức hay khác:

• Giải Toán 7 trang 75 Tập 1
• Giải Toán 7 trang 76 Tập 1
• Giải Toán 7 trang 77 Tập 1
• Giải Toán 7 trang 78 Tập 1