Vẽ tam giác vuông ABC có góc A = 90 độ, AB = 3 cm, BC = 5 cm theo các bước sau: - Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 3 cm
Câu hỏi:
Vẽ tam giác vuông ABC có AB = 3 cm, BC = 5 cm theo các bước sau:
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 3 cm.
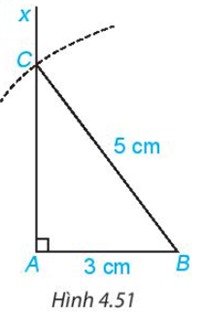
- Vẽ tia Ax vuông góc với AB và cung tròn tâm B bán kính 5 cm như Hình 4.51.
Cung tròn cắt tia Ax tại điểm C.
- Vẽ đoạn thẳng BC ta được tam giác ABC.
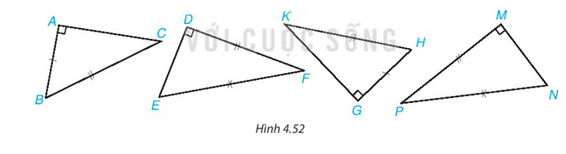
Trả lời:
Ta thực hiện vẽ theo các bước như sau:
Bước 1. Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 3 cm.
Bước 2. Vẽ tia Ax vuông góc với AB tại A.
Bước 3. Vẽ cung tròn tâm B bán kính 5 cm. Cung tròn cắt tia Ax tại điểm C.
Nối BC ta được tam giác ABC.