Bài 2 trang 61 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác - Cánh diều

Bài 2 trang 61 Toán 8 Tập 2: Có thể gián tiếp đo chiều cao của một bức tuờng khá cao bằng dụng cụ đơn giản được không?

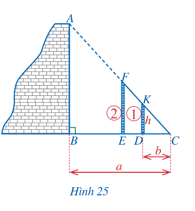
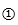
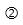
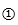
Hình 25 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: hai cọc thẳng đứng (cọc cố định; cọc có thể di động được) và sợi dây FC. Cọc có chiều cao DK = h. Các khoảng cách BC = a, DC = b đo được bằng thước dây thông dụng.

a) Em hãy cho biết người ta tiến hành đo đạc như thế nào?

b) Tính chiều cao AB theo h, a, b.

Lời giải:

a) Cách tiến hành:

⦁ Vì cọc 2 di động được nên di chuyển cọc sao cho cọc trùng với AB, cụ thể F trùng với A, E trùng với B. 

⦁ Lúc này cọc song song với AB. Do đó, ta có tỉ lệ giữa chiều cao của cọc và AB bằng với tỉ lệ giữa khoảng cách DC và BC. Từ đó ta tính được chiều cao AB của bức tường thông qua hệ quả của định lí Thalès.

b) Xét ∆ABC với AB // KD (D ∈ BC, K ∈ AC), ta có:

$\frac{\mathrm{DK}}{\mathrm{BA}}=\frac{\mathrm{DC}}{\mathrm{BC}}$ (hệ quả định lí Thalès)

Suy ra $\mathrm{AB}=\frac{\mathrm{DK}\cdot \mathrm{BC}}{\mathrm{DC}}=\frac{h\cdot a}{b}$

Vậy chiều cao $\mathrm{AB}=\frac{\mathrm{ha}}{b}.$

Lời giải bài tập Toán 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác hay, chi tiết khác:

• Khởi động trang 58 Toán 8 Tập 2: Từ xa xưa, con người đã muốn tìm hiểu về Mặt Trời, Trái Đất, Mặt Trăng ....

• Luyện tập 1 trang 59 Toán 8 Tập 2: Bạn Loan đặt một cái que lên bàn cờ vua như ở Hình 20. Bạn ấy nói rằng ....

• Luyện tập 2 trang 60 Toán 8 Tập 2: Người ta đo bóng của một cây và được các số đo ở Hình 23. Giả sử rằng các tia nắng song song với nhau ....

• Bài 1 trang 60 Toán 8 Tập 2: Để đo khoảng cách giữa hai vị trí A và B trong đó B không tới được ....

• Bài 3 trang 61 Toán 8 Tập 2: Trong Hình 26, các thanh AA’, BB’, CC’, DD’ của giàn gỗ song song với nhau ....

• Bài 4 trang 61 Toán 8 Tập 2: Anh Thiện và chị Lương đứng ở hai phía bờ sông và muốn ước lượng khoảng cách giữa hai vị trí ....