Luyện tập 2 trang 84 Toán 8 Tập 2 Cánh diều

Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh HA.HD = HB.HE.

Giải Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác - Cánh diều

Luyện tập 2 trang 84 Toán 8 Tập 2: Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh HA.HD = HB.HE.

Lời giải:

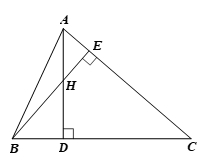
Do tam giác ABC có hai đường cao AD và BE nên BE ⊥ AC, AD ⊥ BC.

Suy ra $\widehat{\mathrm{AEB}}=\widehat{\mathrm{ADB}}=90°$ hay $\widehat{\mathrm{AEH}}=\widehat{\mathrm{BDH}}=90°$

Xét ∆HEA và ∆HDB có:

$\widehat{\mathrm{AEH}}=\widehat{\mathrm{BDH}}=90°;$

$\widehat{\mathrm{AHE}}=\widehat{\mathrm{BHD}}$ (đối đỉnh)

Suy ra ∆HEA ᔕ ∆HDB (g.g).

Do đó $\frac{\mathrm{HE}}{\mathrm{HD}}=\frac{\mathrm{HA}}{\mathrm{HB}}$ (tỉ số đồng dạng)

Vì vậy, HA.HD = HB.HE.

Lời giải bài tập Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác hay, chi tiết khác:

• Khởi động trang 83 Toán 8 Tập 2: Bạn Khanh vẽ hai tam giác ABC và A’B’C’ sao cho $\widehat{A^{\text{'}}}=\hat{A}=60°$ và $\hat{B}=\widehat{B^{\text{'}}}=45°$ (Hình 79) ....

• Hoạt động 1 trang 83 Toán 8 Tập 2: Cho hai tam giác ABC, A’B’C’ sao cho: $\hat{A}=\widehat{A^{\text{'}}},\hat{B}=\widehat{B^{\text{'}}}$ và A’B’ ≠ AB (Hình 80) ....

• Luyện tập 1 trang 83 Toán 8 Tập 2: Cho hai tam giác ABC và MNP thỏa mãn: $\hat{A}=50°,$ $\hat{B}=60°,$ $\hat{N}=60°,$ $\hat{P}=70°$ ....

• Hoạt động 2 trang 84 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ có $\widehat{A^{\text{'}}}=\hat{A}=90°,$ $\widehat{B^{\text{'}}}=\hat{B}$ (Hình 84) ....

• Bài 1 trang 85 Toán 8 Tập 2: Cho Hình 86. a) Chứng minh ∆MNP ᔕ ∆ABC. b) Tìm x ....

• Bài 2 trang 85 Toán 8 Tập 2: Cho hai tam giác ABC và PMN thỏa mãn $\hat{A}=70°,$ $\hat{B}=80°,$ $\hat{M}=80°,$ $\hat{N}=30°.$ ....

• Bài 3 trang 85 Toán 8 Tập 2: Cho tam giác nhọn ABC, hai đường cao AD và BE cắt nhau tại H. Chứng minh: ....

• Bài 4 trang 85 Toán 8 Tập 2: Cho Hình 87 với $\widehat{\mathrm{OAD}}=\widehat{\mathrm{OCB}}.$ Chứng minh: a) ∆OAD ᔕ ∆OCB; ....

• Bài 5 trang 85 Toán 8 Tập 2: Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh: ....

• Bài 6 trang 85 Toán 8 Tập 2: Cho Hình 89, bạn Minh dùng một dụng cụ để đo chiều cao của cây ....