Luyện tập 3 trang 55 Toán 8 Tập 2 Cánh diều

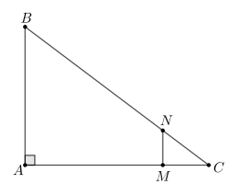
Cho tam giác ABC vuông tại A có CA = 4, CB = 5. Giả sử M, N là hai điểm lần lượt nằm trên hai cạnh CA, CB sao cho CM = 1, CN = 1,25. Tính độ dài đoạn thẳng MN.

Giải Toán 8 Bài 1: Định lí Thalès trong tam giác - Cánh diều

Luyện tập 3 trang 55 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có CA = 4, CB = 5. Giả sử M, N là hai điểm lần lượt nằm trên hai cạnh CA, CB sao cho CM = 1, CN = 1,25. Tính độ dài đoạn thẳng MN.

Lời giải:

Ta có: $\frac{\mathrm{CN}}{\mathrm{CB}}=\frac{1,25}{5}=\frac{1}{4}$ và $\frac{\mathrm{CM}}{\mathrm{CA}}=\frac{1}{4}.$

Do đó, $\frac{\mathrm{CN}}{\mathrm{CB}}=\frac{\mathrm{CM}}{\mathrm{CA}}\left(=\frac{1}{4}\right).$

Trong ∆ABC, có $\frac{\mathrm{CN}}{\mathrm{CB}}=\frac{\mathrm{CM}}{\mathrm{CA}}$

Suy ra MN // AB (định lí Thalès đảo)

Mà AB ⊥ AC (do tam giác ABC vuông tại A) nên MN ⊥ AC tại M.

Xét ∆MNC vuông tại M có:CN² = CM²+ MN²(định lí Pythagore)

Suy ra, $\mathrm{MN}=\sqrt{{\mathrm{CN}}^2-{\mathrm{CM}}^2}=\sqrt{1,{25}^2-1^2}=0,75\left(\text{cm}\right).$

Lời giải bài tập Toán 8 Bài 1: Định lí Thalès trong tam giác hay, chi tiết khác:

• Khởi động trang 52 Toán 8 Tập 2: Bác Dư muốn cắt một thanh sắt (Hình 1) thành 5 phần bằng nhau ....

• Hoạt động 1 trang 52 Toán 8 Tập 2: Cho hai đoạn thẳng AB = 2 cm, CD = 3 cm và hai đoạn thẳng MN = 4 cm, PQ = 6 cm ....

• Hoạt động 2 trang 53 Toán 8 Tập 2: Quan sát Hình 3 và cho biết: Đường thẳng d có song song với BC hay không ....

• Luyện tập 1 trang 53 Toán 8 Tập 2: Trong Hình 4, chứng tỏ rằng nếu MN // BC thì MB/AB = NC/AC ....

• Luyện tập 2 trang 53 Toán 8 Tập 2: Cho tam giác ABC có G là trọng tâm. Đường thẳng qua G song song với BC ....

• Hoạt động 3 trang 54 Toán 8 Tập 2: Trong Hình 7, cho AM = 1, MB = 2, AN = 1,5, NC = 3 ....

• Bài 1 trang 57 Toán 8 Tập 2: Cho tam giác ABC có AB = 4,5 cm; AC = 6 cm. Các điểm M, N lần lượt thuộc ....

• Bài 2 trang 57 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có AB = 4 cm, CD = 6 cm ....

• Bài 3 trang 57 Toán 8 Tập 2: Trong Hình 15, cho MN // AB, NP // BC. Chứng minh MP // AC ....

• Bài 4 trang 57 Toán 8 Tập 2: Trong Hình 16, độ dài đoạn thẳng A’C’ mô tả chiều cao của một cái cây ....

• Bài 5 trang 57 Toán 8 Tập 2: Cho đoạn thẳng AB. Hãy trình bày cách chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau ....