Giải Toán 8 trang 107 Tập 1 Cánh diều

---

Với Giải Toán 8 trang 107 Tập 1 trong Bài 4: Hình bình hành Toán lớp 8 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 107.

Giải Toán 8 trang 107 Tập 1 Cánh diều

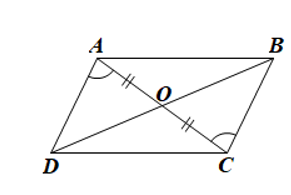
Luyện tập 2 trang 107 Toán 8 Tập 1: Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và $\widehat{OAD}=\widehat{OCB}$. Chứng minh tứ giác ABCD là hình bình hành.

Lời giải:

• Xét ΔOAD và ΔOCB có:

$\widehat{OAD}=\widehat{OCB}$ (giả thiết);

OA = OC (giả thiết);

$\widehat{AOD}=\widehat{COB}$ (đối đỉnh)

Do đó ΔOAD = ΔOCB (g.c.g)

Suy ra OD = OB (hai cạnh tương ứng)

• Xét tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường

Do đó ABCD là hình bình hành.

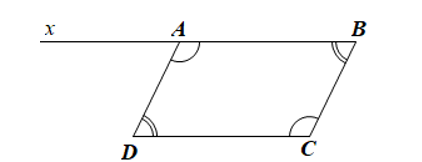
Bài 1 trang 107, 108 Toán 8 Tập 1: Cho tứ giác ABCD có $\widehat{DAB}=\widehat{BCD},\widehat{ABC}=\widehat{CDA}$. Kẻ tia Ax là tia đối của tia AB. Chứng minh:      

a) $\widehat{ABC}+\widehat{DAB}=180º$;

b) $\widehat{xAD}=\widehat{ABC}$; AD // BC;

c) Tứ giác ABCD là hình bình hành.

Lời giải:

a) Xét tứ giác ABCD có:

$\widehat{DAB}+\widehat{ABC}+\widehat{BCD}+\widehat{CDA}=360°$ (tổng các góc của một tứ giác)

Mà $\widehat{DAB}=\widehat{BCD}$, $\widehat{ABC}=\widehat{CDA}$ (giả thiết)

Nên $\widehat{DAB}+\widehat{ABC}+\widehat{DAB}+\widehat{ABC}=360°$

$2\widehat{ABC}+2\widehat{DAB}=360°$

$2\left(\widehat{ABC}+\widehat{DAB}\right)=360°$

$\widehat{ABC}+\widehat{DAB}=180°$.

Vậy $\widehat{ABC}+\widehat{DAB}=180°$.

b) Ta có $\widehat{xAD}+\widehat{DAB}=180°$ (hai góc kề bù)

Mà $\widehat{ABC}+\widehat{DAB}=180°$ (câu a)

Suy ra $\widehat{xAD}=\widehat{ABC}$

Mà hai góc trên ở vị trí đồng vị nên AD // BC.

c) Xét tứ giác ABCD có: $\widehat{DAB}=\widehat{BCD}$, $\widehat{ABC}=\widehat{CDA}$ (giả thiết)

Do đó tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).

Lời giải bài tập Toán 8 Bài 4: Hình bình hành hay khác:

• Giải Toán 8 trang 105

• Giải Toán 8 trang 106

• Giải Toán 8 trang 108