Giải Toán 8 trang 121 Tập 1 Cánh diều

---

Với Giải Toán 8 trang 121 Tập 1 trong Bài tập cuối chương 5 Toán lớp 8 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 121.

Giải Toán 8 trang 121 Tập 1 Cánh diều

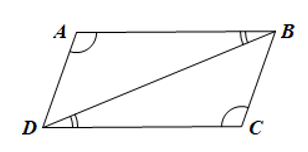
Bài 7 trang 121 Toán 8 Tập 1: Cho tứ giác ABCD có $\widehat{DAB}=\widehat{BCD},\widehat{ABD}=\widehat{CDB}$. Chứng minh ABCD là hình bình hành.

Lời giải:

Ta có $\widehat{ABD}=\widehat{CDB}$ mà hai góc này ở vị trí so le trong nên AB // CD.

Từ AB // CD, suy ra $\left\{\begin{array}{l}\widehat{CDA}+\widehat{DAB}=180°\\ \widehat{ABC}+\widehat{BCD}=180°\end{array}\right.$ (các cặp góc trong cùng phía)

Lại có $\widehat{DAB}=\widehat{BCD}$ nên $\widehat{CDA}=\widehat{ABC}$.

Xét tứ giác ABCD có $\widehat{DAB}=\widehat{BCD}$ (giả thiết) và $\widehat{CDA}=\widehat{ABC}$ (chứng minh trên)

Suy ra ABCD là hình bình hành (các cặp góc đối bằng nhau).

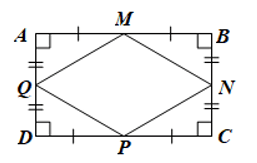
Bài 8 trang 121 Toán 8 Tập 1: Cho hình chữ nhật ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác MNPQ là hình thoi.

Lời giải:

• Vì ABCD là hình chữ nhật nên AB = CD và AD = BC.

Vì M là trung điểm của AB nên $MA=MB=\frac{1}{2}AB$;

      N là trung điểm của CD nên $PC=PD=\frac{1}{2}CD$

Do đó MA = MB = PC = PD.

Tương tự ta cũng có QA = QD = NB = NC.

• Xét ΔAMQ và ΔBMN có:

$\widehat{MAQ}=\widehat{MBN}=90°$ (do ABCD là hình chữ nhật);

MA = MB (chứng minh trên);

QA = NB (chứng minh trên)

Do đó ΔAMQ = ΔBMN (hai cạnh góc vuông)

Suy ra MQ = MN (hai cạnh tương ứng)      (1)

Chứng minh tương tự, ta có:

+) ΔBMN = ΔCPN (hai cạnh góc vuông)

Suy ra MN = PN (hai cạnh tương ứng)      (2)

+) ΔCPN = ΔDPQ (hai cạnh góc vuông)

Suy ra PN = PQ (hai cạnh tương ứng)      (3)

Từ (1), (2) và (3) suy ra MN = PN = PQ = MQ.

• Tứ giác MNPQ có MN = PN = PQ = MQ nên là hình thoi.

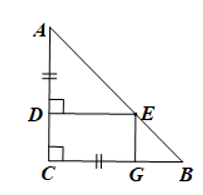
Bài 9 trang 121 Toán 8 Tập 1: Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao cho AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.

Lời giải:

Vì ΔABC vuông cân tại C (giả thiết) nên $\widehat{A}=\widehat{B}=45°$.

Xét ΔADE vuông tại D (do DE ⊥ AC) có:

$\widehat{DAE}+\widehat{DEA}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $\widehat{DEA}=90°-\widehat{DAE}=90°-45°=45°$

ΔADE vuông tại D có $\widehat{DAE}=\widehat{DEA}$ (cùng bằng 45°) nên là tam giác vuông cân tại D

Do đó AD = ED.

Mà AD = CG nên ED = CG.

Xét tứ giác CDEG có:

• ED = CG (chứng minh trên);

• ED // CG (do cùng vuông góc với AC)

Do đó CDEG là hình bình hành

Lại có $\widehat{CDE}=90°$

  Suy ra CDEG là hình chữ nhật.

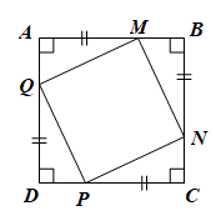
Bài 10 trang 121 Toán 8 Tập 1: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.

Lời giải:

• Do ABCD là hình vuông nên AB = BC = CD = DA.

Mà AM = BN = CP = DQ

Suy ra AB – AM = BC – BN = CD – CP = DA – DQ

Hay MB = NC = PD = QA

• Xét ΔAMQ và ΔBNM có:

$\widehat{MAQ}=\widehat{NBM}=90°$;

AM = BN (giả thiết);

QA = MB (chứng minh trên)

Do đó ΔAMQ = ΔBNM (hai cạnh góc vuông)

Suy ra QM = MN (hai cạnh tương ứng).

Chứng minh tương tự ta có: MN = NP và NP = PQ.

Khi đó MN = NP = PQ = QM.

• Tứ giác MNPQ có 4 cạnh bằng nhau nên là hình thoi.

• Do ΔAMQ = ΔBNM (chứng minh trên) nên $\widehat{AMQ}=\widehat{BNM}$ (hai góc tương ứng)

Mà $\widehat{BNM}+\widehat{BMN}=90°$ (do ΔBMN vuông tại B)

Suy ra $\widehat{AMQ}+\widehat{BMN}=90°$

Lại có $\widehat{AMQ}+\widehat{QMN}+\widehat{BMN}=180°$

Suy ra $\widehat{QMN}=180°-\left(\widehat{AMQ}+\widehat{BMN}\right)=180°-90°=90°$.

• Hình thoi MNPQ có $\widehat{QMN}=90°$ nên là hình vuông.

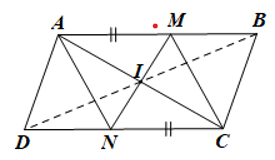
Bài 11 trang 121 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh:

a) ΔIAM = ΔICN;

b) Tứ giác AMCN là hình bình hành;

c) Ba điểm B, I, D thẳng hàng.

Lời giải:

a) Do ABCD là hình bình hành nên AB // CD.

Suy ra $\widehat{AMN}=\widehat{CNM}$ và $\widehat{MAC}=\widehat{NCM}$ (các cặp góc so le trong)

Xét ΔIAM và ΔICN có:

$\widehat{AMI}=\widehat{CNI}$ (do $\widehat{AMN}=\widehat{CNM}$);

AM = CN (giả thiết);

$\widehat{MAI}=\widehat{NCI}$ (do $\widehat{MAC}=\widehat{NCM}$)

Do đó ΔIAM = ΔICN (g.c.g)

b) Xét tứ giác AMCN có AM = CN (giả thiết) và AM // CN (do AB // CD)

Suy ra tứ giác AMCN là hình bình hành.

c) Do AMCN là hình bình hành nên hai đường chéo AC, MN cắt nhau tại trung điểm I của mỗi đường.

Do ABCD là hình bình hành nên hai đường chéo AC, BD cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của AC nên I là trung điểm của BD.

Do đó ba điểm B, I, D thẳng hàng.

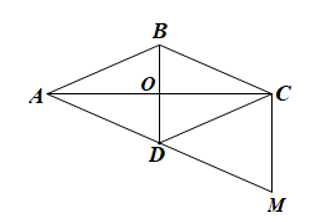
Bài 12 trang 121 Toán 8 Tập 1: Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:

a) $OD=\frac{1}{2}CM$ và tam giác ACM là tam giác vuông;

b) Ba điểm A, D, M thẳng hàng;

c) Tam giác DCM là tam giác cân.

Lời giải:

a) • Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.

Suy ra $OD=\frac{1}{2}BD$.

Do BCMD là hình bình hành nên BD = CM.

Do đó $OD=\frac{1}{2}CM$.

• Ta có: CM // BD (do BCMD là hình bình hành)

              AC ⊥ BD (chứng minh trên)

Do đó CM ⊥ AC hay $\widehat{MCA}=90°$

Vây tam giác ACM là tam giác vuông.

b) Vì ABCD là hình thoi nên AD // BC

Vì BCMD là hình bình hành nên DM // BC

Do đó qua điểm D có hai đường thẳng AD và DM cùng song song với đường thẳng BC nên AD trùng với DM (Tiên đề Euclid)

Hay ba điểm A, D, M thẳng hàng.

c) Ta có: BD // CM (chứng minh câu a) nên:

• $\widehat{BDC}=\widehat{DCM}$ (so le trong);   (1)

• $\widehat{ADB}=\widehat{DMC}$ (đồng vị)         (2)

Do ABCD là hình thoi nên DB là tia phân giác của góc ADC

Do đó $\widehat{ADB}=\widehat{BDC}$                 (3)

Từ (1), (2) và (3) suy ra $\widehat{DCM}=\widehat{DMC}$.

Xét ΔDCM có $\widehat{DCM}=\widehat{DMC}$ nên là tam giác cân tại D.

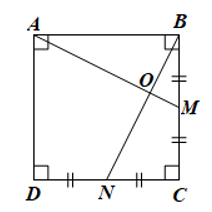
Bài 13 trang 121 Toán 8 Tập 1: Cho hình vuông ABCD có M, N lần lượt là trung điểm của các cạnh BC, CD. Gọi O là giao điểm của AM và BN. Chứng minh:

a) ΔABM = ΔBCN;

b) $\widehat{BAO}=\widehat{MBO}$;

c) AM ⊥ BN.

Lời giải:

a) Do ABCD là hình vuông nên AB = BC = CD = DA.

Vì M là trung điểm của BC nên $MB=MC=\frac{1}{2}BC$;

     N là trung điểm của CD nên $NC=ND=\frac{1}{2}CD$.

Do đó MB = MC = NC = ND.

Xét ΔABM và ΔBCN có:

$\widehat{ABM}=\widehat{BCN}=90°$ (do ABCD là hình vuông);

AB = CD (chứng minh trên);

MB = NC (chứng minh trên)

Do đó ΔABM = ΔBCN (hai cạnh góc vuông).

b) Vì ΔABM = ΔBCN (câu a) nên $\widehat{BAM}=\widehat{CBN}$ (hai góc tương ứng).

Hay $\widehat{BAO}=\widehat{MBO}$.

c) Xét ΔABM vuông tại B có $\widehat{BAO}+\widehat{BMO}=90°$

Mà $\widehat{BAO}=\widehat{MBO}$ (câu b) nên $\widehat{MBO}+\widehat{BMO}=90°$.

Xét ΔMBO có $\widehat{MBO}+\widehat{BMO}+\widehat{BOM}=180°$ (tổng ba góc trong một tam giác)

Suy ra $\widehat{BOM}=180°-\left(\widehat{MBO}+\widehat{BMO}\right)=180°-90°=90°$.

Do đó OM ⊥ BO hay AM ⊥ BN.

Lời giải bài tập Toán 8 Bài tập cuối chương 5 hay khác:

• Giải Toán 8 trang 120