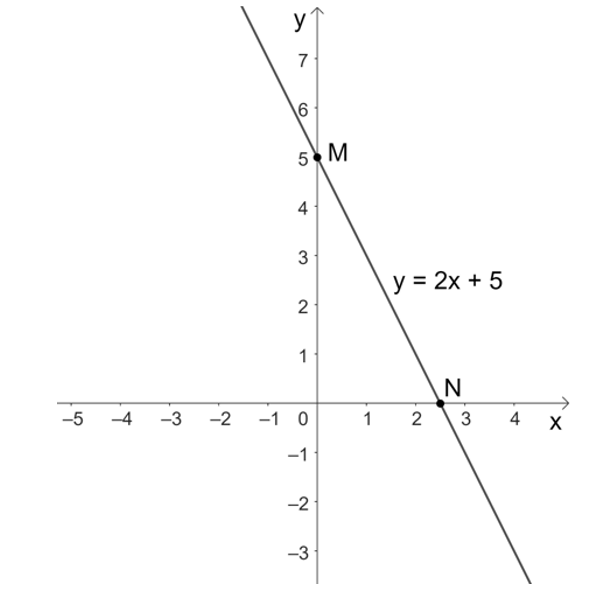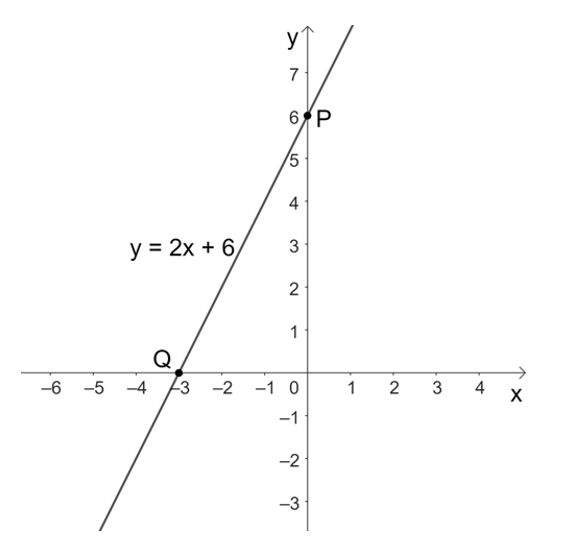Giải Toán 8 trang 79 Tập 1 Cánh diều
Với Giải Toán 8 trang 79 Tập 1 trong Bài tập cuối chương 3 Toán lớp 8 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 79.
Giải Toán 8 trang 79 Tập 1 Cánh diều
Bài 5 trang 79 Toán 8 Tập 1: a) Biết rằng với x = 3 thì hàm số y = 2x + b có giá trị là 11. Tìm b và vẽ đồ thị của hàm số với giá trị b vừa tìm được.
b) Biết rằng đồ thị của hàm số y = ax + 6 đi qua điểm A(− 2; 2). Tìm a và vẽ đồ thị của hàm số với giá trị a vừa tìm được.
Lời giải:
a) Với x = 3 thì hàm số y = 2x + b có giá trị là 11 tức là
2 . 3 + b = 11
6 + b = 11
b = 11 – 6 = 5.
Khi đó, ta có đồ thị của hàm số y = 2x + 5.
• Với x = 0 thì y = 2 . 0 + 5 = 0 + 5 = 5, ta được điểm M(0; 5) thuộc đồ thị của hàm số y = 2x + 5.
• Với y = 0 thì 2x + 5 = 0 suy ra , ta được điểm thuộc đồ thị của hàm số y = 2x + 5.
Do đó, đồ thị của hàm số y = 2x + 5 là đường thẳng đi qua hai điểm M(0; 5) và
Ta vẽ đồ thị của hàm số y = 2x + 5 như sau:
b) Đồ thị của hàm số y = ax + 6 đi qua điểm A(− 2; 2) nên – 2a + 6 = 2
Suy ra – 2a = – 4 do đó a = 2.
Khi đó, đồ thị của hàm số cần tìm là y = 2x + 6.
• Với x = 0 thì y = 2 . 0 + 6 = 0 + 6 = 6, ta được điểm P(0; 6) thuộc đồ thị của hàm số y = – 2x + 6.
• Với y = 0 thì 2x + 6 = 0 suy ra x = – 3, ta được điểm Q(– 3; 0) thuộc đồ thị của hàm số y = – 2x + 6.
Do đó, đồ thị của hàm số y = 2x + 6 là đường thẳng đi qua hai điểm P(0; 6) và Q(– 3; 0).
Ta vẽ đồ thị của hàm số y = 2x + 6 như sau:
Bài 6 trang 79 Toán 8 Tập 1: >Tìm hàm số bậc nhất y = ax + b (a ≠ 0) trong mỗi trường hợp sau:
a) Đồ thị của hàm số đó đi qua điểm M(1; 3) và có hệ số góc bằng – 2;
b) Đồ thị của hàm số đó đi qua điểm N(– 1; 4) và song song với đường thẳng y = –3x – 1.
Lời giải:
a) Hàm số bậc nhất y = ax + b có hệ số góc bằng – 2 nên có dạng y = – 2x + b.
Đồ thị của hàm số y = – 2x + b đi qua điểm M(1; 3) thì ta có:
– 2 . 1 + b = 3 suy ra b = 5.
Vậy hàm số bậc nhất cần tìm là y = – 2x + 5.
b) Đồ thị của hàm số y = ax + b song song với đường thẳng y = –3x – 1 nên có dạng y = –3x + b.
Đồ thị của hàm số y = –3x + b đi qua điểm N(– 1; 4) thì ta có:
(–3) . (– 1) + b = 4
3 + b = 4
Suy ra b = 1.
Vậy hàm số bậc nhất cần tìm là y = – 3x + 1.
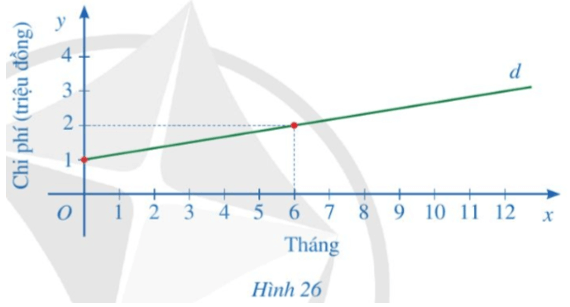
Bài 7 trang 79 Toán 8 Tập 1: Để sử dụng dịch vụ truyền hình cáp, người dùng phải trả một khoản phí ban đầu và phí thuê bao hằng tháng. Một phần đường thẳng d ở Hình 26 biểu thị tổng chi phí (đơn vị: triệu đồng) để sử dụng dịch vụ truyền hình cáp theo thời gian sử dụng của một gia đình (đơn vị: tháng).
a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng d.
b) Giao điểm của đường thẳng d với trục tung trong tình huống này có ý nghĩa gì?
c) Tính tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng.
Lời giải:
a) Gọi đường thẳng d có dạng y = ax + b.
Trong đó: y là chi phí sử dụng dịch vụ truyền hình cáp (triệu đồng) trong x (tháng).
• Với x = 0 thì y = 1 nên ta có 0x + b = 1 hay b = 1.
Khi đó, hàm số bậc nhất có dạng y = ax + 1.
• Với x = 6 thì y = 2 nên ta có 6a + 1 = 2 hay 6a = 1 suy ra .
Vậy hàm số bậc nhất biểu diễn đường thẳng d là .
b) Giao điểm của đường thẳng d với trục tung trong tình huống này là chi phí ban đầu để sử dụng dịch vụ truyền hình cáp là 1 triệu đồng.
c) Tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là:
(triệu đồng).
Vậy tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là 3 triệu đồng.
Bài 8 trang 79 Toán 8 Tập 1: Một kho chứa 60 tấn xi măng, mỗi ngày đều xuất đi m (tấn) với 0 < m < 60. Gọi y (tấn) là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.
a) Chứng tỏ rằng y là hàm số bậc nhất của biến x, tức là y = ax + b (a ≠ 0).
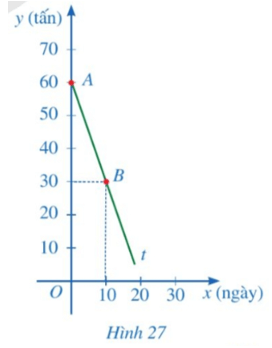
b) Trong Hình 27, tia At là một phần đường thẳng y = ax + b. Tìm a, b. Từ đó hãy cho biết trong kho còn lại bao nhiêu tấn xi măng sau 15 ngày.
Lời giải:
a) Theo đề bài, mỗi ngày đều xuất đi m (tấn) với 0 < m < 60.
Khi đó, khối lượng xi măng sau x ngày xuất hàng là: mx (tấn).
Khối lượng xi măng còn lại trong kho sau x ngày xuất hàng là: 60 – mx (tấn)
Mà y (tấn) cũng là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.
Do đó, y = 60 – mx hay y = – mx + 60.
Vậy y là hàm số bậc nhất của biến x.
b) Trong Hình 27, ta thấy:
• Điểm A(0; 60):
Với x = 0 thì y = 60 nên ta có: 0x + b = 60 hay b = 60.
Khi đó, đường thẳng cần tìm có dạng y = ax + 60.
• Điểm B(10; 30):
Với x = 10 thì y = 30 nên ta có: 10a + 60 = 30 hay 10a = – 30 suy ra a = – 3.
Khi đó, đường thẳng cần tìm có dạng y = – 3x + 60.
Do đó, số tấn xi măng trong kho còn lại sau 15 ngày là: – 3 . 15 + 60 = 15 (tấn).
Vậy a = – 3; b = 60 và trong kho còn lại 15 tấn xi măng sau 15 ngày.
Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay khác: