Giải Toán 8 trang 94 Tập 2 Cánh diều

---

Với Giải Toán 8 trang 94 Tập 2 trong Bài tập cuối chương 8 Toán 8 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 94.

Giải Toán 8 trang 94 Tập 2 Cánh diều

Bài 1 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP, $\hat{E}=60°,$ $\hat{M}=40°.$

a) Số đo góc D bằng bao nhiêu độ?

A. 40°.       

B. 50°.       

C. 60°.       

D. 80°.

b) Số đo góc N bằng bao nhiêu độ?

A. 40°.       

B. 50°.       

C. 60°.       

D. 80°.

c) Số đo góc P bằng bao nhiêu độ?

A. 40°.       

B. 50°.       

C. 60°.       

D. 80°.

Lời giải:

a) Đáp án đúng là: A

Vì ∆DEG ᔕ ∆MNP nên $\hat{D}=\hat{M}=40°$  (hai góc tương ứng).

b) Đáp án đúng là: C    

Vì ∆DEG ᔕ ∆MNP nên $\hat{E}=\hat{N}$  (hai góc tương ứng).

Do đó $\hat{N}=\hat{E}=60°.$

c) Đáp án đúng là: D

Xét tam giác MNP có $\hat{M}+\hat{N}+\hat{P}=180°$  (tổng ba góc của một tam giác)

Suy ra $\hat{P}=180°-\left(\hat{M}+\hat{N}\right)=180°-\left(40°+60°\right)=80°.$

Bài 2 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP, DE = 2 cm, DG = 4 cm, MN = 4 cm, NP = 6 cm.

a) Độ dài cạnh EG là

A. 2 cm.     

B. 3 cm.     

C. 4 cm.     

D. 8 cm.

b) Độ dài cạnh MP là

A. 2 cm.     

B. 3 cm.     

C. 4 cm.     

D. 8 cm.

Lời giải:

Đáp án đúng là: B

a) Vì ∆DEG ᔕ ∆MNP nên $\frac{\mathrm{DE}}{\mathrm{MN}}=\frac{\mathrm{EG}}{\mathrm{NP}}$  (tỉ số đồng dạng)

Hay $\frac{2}{4}=\frac{\mathrm{EG}}{6}$

Suy ra $\mathrm{EG}=\frac{2\cdot 6}{4}=3$  (cm).

b) Đáp án đúng là: D

Vì ∆DEG ᔕ ∆MNP nên $\frac{\mathrm{DE}}{\mathrm{MN}}=\frac{\mathrm{DG}}{\mathrm{MP}}$  (tỉ số đồng dạng)

Hay $\frac{2}{4}=\frac{4}{\mathrm{MP}}$

Suy ra $\mathrm{MP}=\frac{4\cdot 4}{2}=8$  (cm).

Bài 3 trang 94 Toán 8 Tập 2: Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC, BC sao cho tứ giác BMNP là hình bình hành (Hình 102). Chứng minh rằng $\frac{\mathrm{MN}}{\mathrm{BC}}+\frac{\mathrm{NP}}{\mathrm{AB}}=1.$

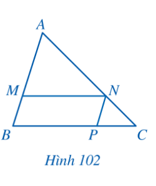
Lời giải:

Vì BMNP là hình bình hành nên NP = MB và MN // BP.

Xét ∆ABC với MN // BC, ta có $\frac{\mathrm{MN}}{\mathrm{BC}}=\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$  (hệ quả của định lí Thalès)

Suy ra $\frac{\mathrm{MN}}{\mathrm{BC}}+\frac{\mathrm{NP}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AB}}+\frac{\mathrm{NP}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AB}}+\frac{\mathrm{MB}}{\mathrm{AB}}=\frac{\mathrm{AM}+\mathrm{MB}}{\mathrm{AB}}=\frac{\mathrm{AB}}{\mathrm{AB}}=1$ .

Vậy $\frac{\mathrm{MN}}{\mathrm{BC}}+\frac{\mathrm{NP}}{\mathrm{AB}}=1.$

Bài 4 trang 94 Toán 8 Tập 2: Cho tứ giác ABCD. Tia phân giác của góc BAD và BCD cắt nhau tại điểm I (Hình 103). Chứng minh AB.CD = AD.BC.

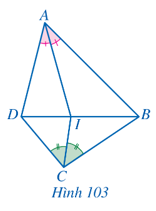
Lời giải:

Xét ∆ABD có AI là phân giác của góc BAD nên $\frac{\mathrm{IB}}{\mathrm{ID}}=\frac{\mathrm{AB}}{\mathrm{AD}}$  (tính chất đường phân giác)

Xét ∆BCD có CI là phân giác của góc BCD nên $\frac{\mathrm{IB}}{\mathrm{ID}}=\frac{\mathrm{CB}}{\mathrm{CD}}$  (tính chất đường phân giác)

Bài 5 trang 94 Toán 8 Tập 2: Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:

a) MP // AD, $\mathrm{MP}=\frac{1}{4}\mathrm{AD};$

b) $\mathrm{AQ}=\frac{2}{5}\mathrm{AN};$

c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và  $\mathrm{PR}=\frac{3}{4}\mathrm{AD}.$  

Lời giải:

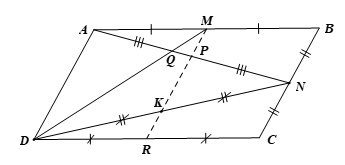
a)  Do N là trung điểm của BC nên $\mathrm{BN}=\frac{1}{2}\mathrm{BC}$

Và ABCD là hình bình hành nên BC = AD, BC // AD

Suy ra  $\mathrm{BN}=\frac{1}{2}\mathrm{AD},\mathrm{BN}\text{ // }\mathrm{AD}$ (1)

Xét ∆ABN có M, P lần lượt là trung điểm của AB, AN nên MP là đường trung bình của ∆ABN

Suy ra $\mathrm{MP}=\frac{1}{2}\mathrm{BN}$  và MP // BN         (2)

Từ (1) và (2) ta có $\mathrm{MP}=\frac{1}{2}\mathrm{BN}=\frac{1}{2}\cdot \frac{1}{2}\mathrm{AD}=\frac{1}{4}\mathrm{AD}$  và MP // AD.

Vậy MP // AD và $\mathrm{MP}=\frac{1}{4}\mathrm{AD}.$  (3)

b) Xét ∆ADQ với MP // AD, ta có $\frac{\mathrm{AD}}{\mathrm{MP}}=\frac{\mathrm{QA}}{\mathrm{QP}}$  (hệ quả của định lí Thalès)

Hay $\frac{\mathrm{AD}}{\frac{1}{4}\mathrm{AD}}=\frac{\mathrm{AQ}}{\mathrm{PQ}}$  nên $\frac{\mathrm{AQ}}{\mathrm{PQ}}=\frac{4}{1}$

Suy ra $\frac{\mathrm{AQ}}{\mathrm{PQ}+\mathrm{AQ}}=\frac{4}{1+4}$  hay $\frac{\mathrm{AQ}}{\mathrm{AP}}=\frac{4}{5}$

Mà P là trung điểm của AN nên $\mathrm{AP}=\frac{1}{2}\mathrm{AN}$

Do đó $\frac{\mathrm{AQ}}{\frac{1}{2}\mathrm{AN}}=\frac{4}{5},$  suy ra $\mathrm{AQ}=\frac{4}{5}\cdot \frac{1}{2}\mathrm{AN}=\frac{2}{5}\mathrm{AN}.$

Vậy $\mathrm{AQ}=\frac{2}{5}\mathrm{AN}.$

c) Gọi K là trung điểm của DN.

Xét ∆AND có P, K lần lượt là trung điểm của AN, DN nên PK là đường trung bình của ∆AND. Do đó PK // AD và $\mathrm{PK}=\frac{1}{2}\mathrm{AD}$    (4)

Tương tự, xét ∆CDN có KR là đường trung bình của ∆CDN nên KR // CN và $\mathrm{KR}=\frac{1}{2}\mathrm{CN}$    

Mà N là trung điểm của BC nên $\mathrm{CN}=\frac{1}{2}\mathrm{BC}=\frac{1}{2}\mathrm{AD}$  và BC // AD

Do đó KR // AD và $\mathrm{KR}=\frac{1}{2}\mathrm{CN}=\frac{1}{2}\cdot \frac{1}{2}\mathrm{AD}=\frac{1}{4}\mathrm{AD}$  (5)

Từ (3), (4) và (5), theo tiên đề Euclid ta có: M, P, K, R thẳng hàng.

Và $\mathrm{PR}=\mathrm{PK}+\mathrm{KR}=\frac{1}{2}\mathrm{AD}+\frac{1}{4}\mathrm{AD}=\frac{3}{4}\mathrm{AD}.$

Vậy ba điểm M, P, R thẳng hàng và $\mathrm{PR}=\frac{3}{4}\mathrm{AD}.$

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay khác:

• Giải Toán 8 trang 95

• Giải Toán 8 trang 96