Giải Toán 8 trang 95 Tập 2 Cánh diều

---

Với Giải Toán 8 trang 95 Tập 2 trong Bài tập cuối chương 8 Toán 8 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 95.

Giải Toán 8 trang 95 Tập 2 Cánh diều

Bài 6 trang 95 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆A’B’C’ với tỉ số đồng dạng k.

a) Gọi AM, AM’ lần lượt là các đường trung tuyến của ∆ABC và ∆A’B’C’. Chứng minh ∆ABM ᔕ ∆A’B’M’ và $\frac{\mathrm{AM}}{A^{\text{'}}{M}^{\text{'}}}=k.$

b) Gọi AD, AD’ lần lượt là các đường phân giác của ∆ABC và ∆A’B’C’.

Chứng minh ∆ABD ᔕ ∆A’B’D’ và $\frac{\mathrm{AD}}{A^{\text{'}}{D}^{\text{'}}}=k.$

c) Gọi AH, AH’ lần lượt là các đường cao của các tam giác nhọn ABC, A’B’C’. Chứng minh ∆ABH ᔕ ∆A’B’H’ và $\frac{\mathrm{AH}}{A^{\text{'}}{H}^{\text{'}}}=k.$

Lời giải:

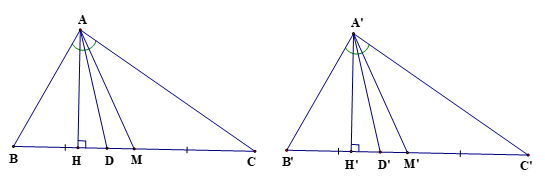
Vì ∆ABC ᔕ ∆A’B’C’với tỉ số đồng dạng k nên ta có:

$\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=\frac{\mathrm{BC}}{B^{\text{'}}{C}^{\text{'}}}=\frac{\mathrm{AC}}{A^{\text{'}}{C}^{\text{'}}}=k$ và $\widehat{\mathrm{BAC}}=\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}},\hat{B}=\widehat{B^{\text{'}}},\hat{C}=\widehat{C^{\text{'}}}.$

a) Vì M, M’ lần lượt là trung điểm của BC, B’C’ nên $\mathrm{BM}=\frac{1}{2}\mathrm{BC}$  và $B^{\text{'}}{M}^{\text{'}}=\frac{1}{2}{B}^{\text{'}}{C}^{\text{'}}$

Suy ra $\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=\frac{\mathrm{BC}}{B^{\text{'}}{C}^{\text{'}}}=\frac{\mathrm{BM}}{B^{\text{'}}{M}^{\text{'}}}=k$

Xét ∆ABM và ∆A’B’M’ có: $\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=\frac{\mathrm{BM}}{B^{\text{'}}{M}^{\text{'}}}=k$  và $\hat{B}=\widehat{B^{\text{'}}}$

Suy ra ∆ABM ᔕ ∆A’B’M’ (c.g.c)

Do đó $\frac{\mathrm{AM}}{A^{\text{'}}{M}^{\text{'}}}=\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=k$  (tỉ số đồng dạng).

b) Vì AD, AD’ lần lượt là các đường phân giác của tam giác ABC, A’B’C’ nên $\widehat{\mathrm{BAD}}=\frac{1}{2}\widehat{\mathrm{BAC}}$  và $\widehat{B^{\text{'}}{A}^{\text{'}}{D}^{\text{'}}}=\frac{1}{2}\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}$

Mà $\widehat{\mathrm{BAC}}=\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}$  nên $\widehat{\mathrm{BAD}}=\widehat{B^{\text{'}}{A}^{\text{'}}{D}^{\text{'}}}$

Xét ∆ABD và ∆A’B’D’ có: $\widehat{\mathrm{BAD}}=\widehat{B^{\text{'}}{A}^{\text{'}}{D}^{\text{'}}}$  và $\hat{B}=\widehat{B^{\text{'}}}$

Do đó ∆ABD ᔕ ∆A’B’D’ (g.g) 

Suy ra $\frac{\mathrm{AD}}{A^{\text{'}}{D}^{\text{'}}}=\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=k$  (tỉ số đồng dạng).

c) Vì AH, AH’ lần lượt là các  đường cao của tam giác ABC, A’B’C’ nên $\widehat{\mathrm{AHB}}=\widehat{A^{\text{'}}{H}^{\text{'}}{B}^{\text{'}}}=90°$

Xét ∆ABH và ∆A’B’H’ có: $\widehat{\mathrm{AHB}}=\widehat{A^{\text{'}}{H}^{\text{'}}{B}^{\text{'}}}=90°$  và $\hat{B}=\widehat{B^{\text{'}}}$

Do đó ∆ABH ᔕ ∆A’B’H’ (g.g)

Suy ra $\frac{\mathrm{AH}}{A^{\text{'}}{H}^{\text{'}}}=\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=k$  (tỉ số đồng dạng).

Bài 7 trang 95 Toán 8 Tập 2: Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c:

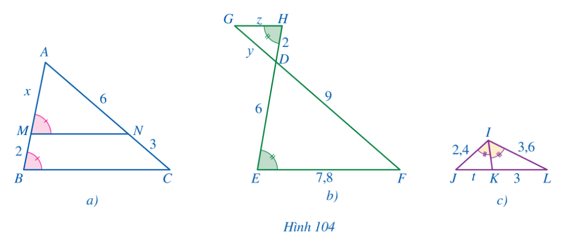
Lời giải:

+ Xét hình 104a:

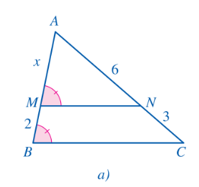
Theo hình vẽ ta có: $\widehat{\mathrm{AMN}}=\widehat{\mathrm{ABC}}$  mà hai góc ở vị trí đồng vị suy ra MN // BC.

Xét ∆ABC với MN // BC, ta có $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}}$  (định lí Thalès)

Hay $\frac{x}{2}=\frac{6}{3}$  nên $x=\frac{2\cdot 6}{3}=4.$

Vậy x = 4.

+ Xét hình 104b:

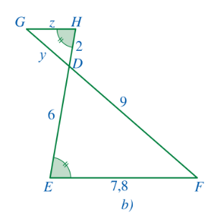
Theo hình vẽ ta có: $\widehat{\mathrm{GHD}}=\widehat{\mathrm{DEF}}$  mà hai góc ở vị trí so le trong nên GH // EF.

Xét ∆DEF với GH // EF, ta có $\frac{\mathrm{GH}}{\mathrm{EF}}=\frac{\mathrm{GD}}{\mathrm{DF}}=\frac{\mathrm{HD}}{\mathrm{DE}}$  (hệ quả của định lí Thalès)

Hay $\frac{z}{7,8}=\frac{y}{9}=\frac{2}{6}$

Suy ra $z=\frac{7,8\cdot 2}{6}=2,6$  và $y=\frac{9\cdot 2}{6}=3.$

Vậy y = 3 và z = 2,6.

+ Xét  hình 104c:

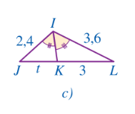
Theo hình vẽ ta có: $\widehat{\mathrm{JIK}}=\widehat{\mathrm{LIK}}$  nên IK là đường phân giác của góc JIL.

Xét ∆IJL có IK là đường phân giác của góc JIL nên $\frac{\mathrm{KJ}}{\mathrm{KL}}=\frac{\mathrm{IJ}}{\mathrm{IL}}$  (tính chất đường phân giác)

Hay $\frac{t}{3}=\frac{2,4}{3,6},$  suy ra $t=\frac{3\cdot 2,4}{3,6}=2.$

Vậy t = 2.

Bài 8 trang 95 Toán 8 Tập 2: Cho Hình 105. Chứng minh:

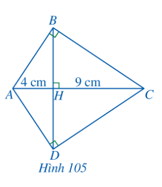
a) ∆HAB ᔕ ∆HBC;

b) HB = HD = 6 cm.

Lời giải:

a) Xét ∆HAB và ∆HBC có:

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{BHC}}=90°;$ $\widehat{\mathrm{HAB}}=\widehat{\mathrm{HBC}}$  (cùng phụ với góc $\widehat{\mathrm{ABH}})$

Suy ra ∆HAB ᔕ ∆HBC (g.g)

b) Do ∆HAB ᔕ ∆HBC (câu a) nên $\frac{\mathrm{HA}}{\mathrm{HB}}=\frac{\mathrm{HB}}{\mathrm{HC}}$  (tỉ số đồng dạng)

Suy ra HB² = HA.HC = 4 . 9 = 36

Do đó HB = 6 cm.

Xét ∆HAD và ∆HDC có

$\widehat{\mathrm{AHD}}=\widehat{\mathrm{DHC}}=90°;$ $\widehat{\mathrm{HAD}}=\widehat{\mathrm{HDC}}$  (cùng phụ với góc $\widehat{\mathrm{ADH}})$

Do đó ∆HAD ᔕ ∆HDC (g.g)

Suy ra $\frac{\mathrm{HA}}{\mathrm{HD}}=\frac{\mathrm{HD}}{\mathrm{HC}}$  (tỉ số đồng dạng)

Nên HD² = HA.HC = 4 . 9 = 36

Do đó HD = 6 (cm).

Vậy HB = HD = 6 cm.

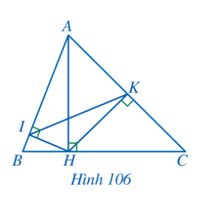
Bài 9 trang 95 Toán 8 Tập 2: Cho Hình 106. Chứng minh:

a) AH² = AB.AI = AC.AK;

b) $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACH}}.$

Lời giải:

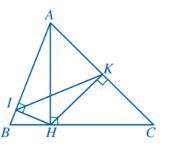
a) Xét ∆AHI và ∆ABH có:

$\widehat{\mathrm{AIH}}=\widehat{\mathrm{AHB}}=90°;$ $\widehat{\mathrm{BAH}}$  là góc chung

Suy ra ∆AHI ᔕ ∆ABH (g.g)

Do đó $\frac{\mathrm{AH}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AH}}$  (tỉ số đồng dạng)

Nên AH² = AB.AI (1)

Xét ∆AHK và ∆ACH có:

$\widehat{\mathrm{AKH}}=\widehat{\mathrm{AHC}}=90°;$ $\widehat{\mathrm{HAC}}$  là góc chung

Suy ra ∆AHK ᔕ ∆ACH (g.g)

Do đó $\frac{\mathrm{AH}}{\mathrm{AC}}=\frac{\mathrm{AK}}{\mathrm{AH}}$  (tỉ số đồng dạng)

Nên AH² = AC.AK (2)

Từ (1) và (2), suy ra AH² = AB.AI = AC.AK.

b) Ta có: AB.AI = AC.AK (câu a) suy ra $\frac{\mathrm{AK}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AC}}$

Xét ∆AIK và ∆ACB có:

$\widehat{\mathrm{BAC}}$ là góc chung; $\frac{\mathrm{AK}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AC}}$ .

Suy ra ∆AIK ᔕ ∆ACB (c.g.c)

Do đó $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACB}}$  (hai góc tương ứng).

Vậy $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACH}}.$

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay khác:

• Giải Toán 8 trang 94

• Giải Toán 8 trang 96