Giải Toán 8 trang 7 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 8 trang 7 Tập 1 trong Bài 1: Đơn thức và đa thức nhiều biến Toán lớp 8 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 7.

Giải Toán 8 trang 7 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 7 Toán 8 Tập 1: Cho các biểu thức sau:

$ab–\pi r^2; \frac{4\pi r^3}{3};\frac{p}{2\pi };x-\frac{1}{y};0;\frac{1}{\sqrt{2}};x^3-x+1$

Trong các biểu thức trên, hãy chỉ ra:

a) Các đơn thức;

b) Các đa thức và số hạng tử của chúng.

Lời giải:

Trong các biểu thức trên:

a) Các đơn thức là: $\frac{4\pi r^3}{3};\frac{p}{2\pi };0;\frac{1}{\sqrt{2}}$.

b) Các đa thức là: $\frac{4\pi r^3}{3};\frac{p}{2\pi };0;\frac{1}{\sqrt{2}}$; ab – πr² và x³ – x + 1.

Các đa thức $\frac{4\pi r^3}{3};\frac{p}{2\pi };0;\frac{1}{\sqrt{2}}$ đều có một hạng tử.

Đa thức ab – πr² có hai hạng tử; đa thức x³ – x + 1 có ba hạng tử.

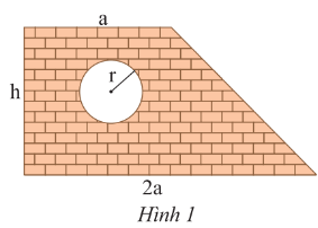
Vận dụng 1 trang 7 Toán 8 Tập 1: Một bức tường hình thang có cửa sổ hình tròn với các kích thước như Hình 1 (tính bằng m).

a) Viết biểu thức biểu thị diện tích bức tường (không tính phần cửa sổ).

b) Tính giá trị diện tích trên khi a = 2 m; h = 3 m; r = 0,5 m (lấy π = 3,14; làm tròn kết quả đến hàng phần trăm).

Lời giải:

a) Biểu thức biểu thị diện tích bức tường hình thang (tính cả phần cửa sổ) là:

$\frac{1}{2}.(a+2a).h=\frac{3}{2} ah$(m²).

Biểu thức biểu thị diện tích của cửa sổ hình tròn là: πr² (m²).

Biểu thức biểu thị diện tích bức tường không tính phần cửa sổ là:

$\frac{3}{2}$ah – πr² (m²).

b) Thay a = 2 m; h = 3 m; r = 0,5 m vào biểu thức ở câu a và lấy π = 3,14 ta có:

$\frac{3}{2}$.2.3 – 3,14.0,5² = 9 – 0,785 = 8,215 (m²).

Làm tròn kết quả đến hàng phần trăm ta được diện tích bức tường không tính phần cửa sổ là 8,22 (m²).

Lời giải bài tập Toán 8 Bài 1: Đơn thức và đa thức nhiều biến Chân trời sáng tạo hay khác:

• Giải Toán 8 trang 6

• Giải Toán 8 trang 9

• Giải Toán 8 trang 10

• Giải Toán 8 trang 11