b) Giả sử một con thuyền di chuyển dọc theo dây cung có độ dài 28 dặm của đường tròn với tâm là tâm của hình quạt tròn,

b) Giả sử một con thuyền di chuyển dọc theo dây cung có độ dài 28 dặm của đường tròn với tâm là tâm của hình quạt tròn, bán kính là 18 dặm. Tính khoảng cách nhỏ nhất từ con thuyền đến hải đăng (theo đơn vị dặm và làm tròn kết quả đến hàng đơn vị).

b) Khoảng cách nhỏ nhất từ con thuyền đến ngọn hải đăng chính là đoạn thẳng vuông góc OH từ ngọn hải đăng (điểm O) đến dây cung CD được mô tả bởi hình vẽ sau:

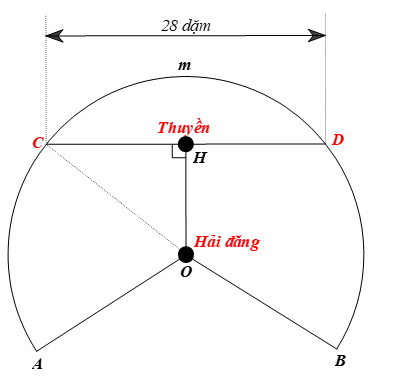
Xét đường tròn (O) có OH ⊥ CD tại H nên theo kết quả câu a, Bài 4, SGK Toán 9, Tập một, trang 124, ta có: H là trung điểm của CD.

Khi đó $CH=\frac{1}{2}CD=\frac{1}{2}\cdot 28=14$  (dặm).

Xét ∆OHC vuông tại H, theo định lí Pythagore, ta có:

OC² = OH² + CH²

Suy ra OH² = OC² – CH² = 18² – 14² = 128.

Do đó $OH=\sqrt{128}\approx 11$  (dặm).

Vậy khoảng cách nhỏ nhất từ thuyền đến ngọn hải đăng khoảng 11 dặm.