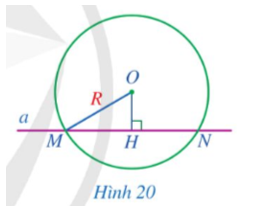
Cho bốn điểm O, M, N, P cùng nằm trên một đường thẳng sao cho điểm M nằm giữa hai điểm O và N;
Câu hỏi:
Cho bốn điểm O, M, N, P cùng nằm trên một đường thẳng sao cho điểm M nằm giữa hai điểm O và N; điểm N nằm giữa hai điểm M và P. Gọi a, b, c lần lượt là các đường thẳng đi qua M, N, P và vuông góc với đường thẳng OP. Xác định vị trí tương đối của mỗi đường thẳng a, b, c và đường tròn (O; ON).
Trả lời:
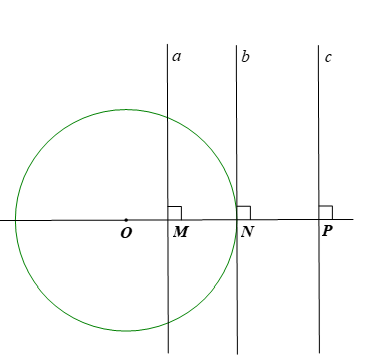
– Vì điểm M nằm giữa hai điểm O và N nên OM < ON suy ra khoảng cách từ O đến đường thẳng a nhỏ hơn bán kính của đường tròn (O; ON). Vậy đường thẳng a và đường tròn (O; ON) cắt nhau.
– Vì khoảng cách từ O đến đường thẳng b (là ON) bằng bán kính của đường tròn (O; ON). Vậy đường thẳng b và đường tròn (O; ON) tiếp xúc nhau.
– Vì điểm M nằm giữa hai điểm O và N; điểm N nằm giữa hai điểm M và P nên điểm N nằm giữa hai điểm O và P.
Suy ra OP > ON nên khoảng cách từ O đến đường thẳng c lớn hơn bán kính của đường tròn (O; ON). Vậy đường thẳng b và đường tròn (O; ON) không giao nhau.