Cho hai đường tròn cùng tâm (O; R), (O; r) với R > r. Các điểm A, B thuộc đường tròn (O; R), các điểm
Câu hỏi:
Cho hai đường tròn cùng tâm (O; R), (O; r) với R > r. Các điểm A, B thuộc đường tròn (O; R), các điểm A’ B’ thuộc đường tròn (O; r) sao cho O, A, A’ thẳng hàng; O, B, B’ thẳng hàng và điểm O không thuộc đường thẳng AB. Chứng minh:
a)
b) AB // A’B’.
Trả lời:
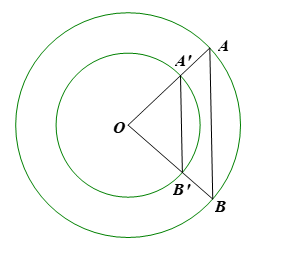
a) Ta có: suy ra
b) Xét ∆OAB có nên AB // A’B’ (theo định lí Thalès đảo).