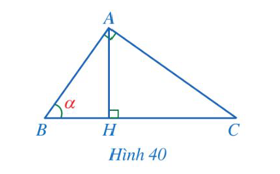
Cho hình thoi ABCD có AB= a , góc BAD = 2a ( 0 độ < a < 90 độ ) Chứng minh: a) BD = 2a.sinα;
Câu hỏi:
Cho hình thoi ABCD có Chứng minh:
a) BD = 2a.sinα;
Trả lời:
a) Gọi O là giao điểm của đường chéo AC và BD.
Vì ABCD là hình thoi nên AC ⊥ BD tại trung điểm O của mỗi đường và AC là đường phân giác của
Suy ra AC = 2AO, BD = 2BO và
Xét ∆ABO vuông tại O, ta có:
Do đó BD = 2BO = 2a.sinα.