Hoạt động 4 trang 70 Toán 9 Tập 2 Cánh diều

Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 8).

Giải Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Cánh diều

Hoạt động 4 trang 70 Toán 9 Tập 2: Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 8).

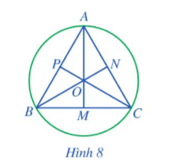
Hoạt động 4 trang 70 Toán 9 Tập 2 Cánh diều | Giải Toán 9

a) AM, BN, CP có là các đường trung trực của tam giác ABC hay không?

b) Điểm O có là tâm đường tròn ngoại tiếp tam giác ABC hay không?

c) Tính AM theo a.

d) Tính OA theo a.

Lời giải:

a) Vì ∆ABC đều nên ba đường trung tuyến AM, BN, CP cũng đồng thời là các đường trung trực của tam giác ABC.

b) Vì ba đường trung trực AM, BN, CP của tam giác ABC cắt nhau tại điểm O nên O là tâm đường tròn ngoại tiếp tam giác ABC.

c) Vì ∆ABC đều nên $\hat{A B M} = \hat{A B C} = 60 ° .$

Xét ∆ABM vuông tại M, ta có:

$A M = A B \cdot s i n \hat{A B M} = a \cdot \sin 60 ° = \frac{a \sqrt{3}}{2} .$

d) Tam giác ABC có AM là đường trung tuyến và O là trọng tâm của tam giác.

Do đó $A O = \frac{2}{3} A M = \frac{2}{3} \cdot \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{3} .$

Vậy $A O = \frac{a \sqrt{3}}{3} .$

Lời giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay, chi tiết khác: