Hoạt động 6 trang 72 Toán 9 Tập 2 Cánh diều
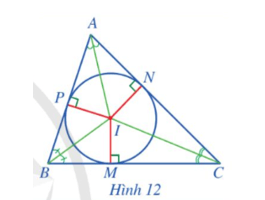
Cho tam giác ABC có I là giao điểm của ba đường phân giác. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (Hình 12).
Giải Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Cánh diều
Hoạt động 6 trang 72 Toán 9 Tập 2: Cho tam giác ABC có I là giao điểm của ba đường phân giác. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (Hình 12).
a) So sánh các đoạn thẳng IM, IN và IP.
b) Đặt r = IM. Đường tròn (I; r) có phải là đường tròn nội tiếp tam giác ABC hay không? Vì sao?
Lời giải:
a) Vì O là giao điểm của ba đường phân giác của tam giác ABC nên điểm O cách đều ba cạnh AB, BC, CA của tam giác ABC.
Do đó IP = IM = IN.
b) Ta có IM = IN = IP = r nên ba điểm M, N, P cùng nằm trên đường tròn (O; r).
Lại có IM ⊥ BC, IN ⊥ AC, IP ⊥ AB nên đường tròn (O; r) tiếp xúc với ba cạnh BC, AC, AB.
Vậy đường tròn (O; r) là đường tròn nội tiếp tam giác ABC.
Lời giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay, chi tiết khác: