Giải Toán 9 trang 42 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 42 Tập 2 trong Bài tập cuối chương 6 Toán 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 42.

Giải Toán 9 trang 42 Tập 2 Cánh diều

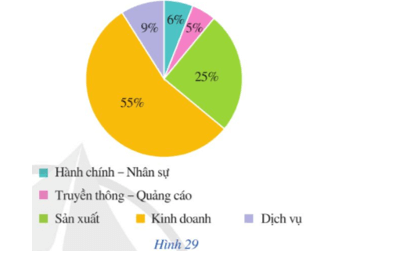
Bài 6 trang 42 Toán 9 Tập 2: Mỗi nhân viên của một công ty làm việc ở một trong năm bộ phận của công ty đó là: Hành chính – Nhân sự; Truyền thông – Quảng cáo; Kinh doanh; Sản xuất; Dịch vụ.

Biểu đồ hình quạt tròn trong Hình 29 thống kê tỉ lệ nhân viên thuộc mỗi bộ phận.

Chọn ngẫu nhiên một nhân viên của công ty. Tính xác suất của mỗi biến cố sau:

A: “Nhân viên được chọn thuộc bộ phận Kinh doanh”;

B: “Nhân viên được chọn không thuộc bộ phận Hành chính – Nhân sự hay Dịch vụ”.

Lời giải:

Xét phép thử: “Chọn ngẫu nhiên một nhân viên của công ty”.

Ta thấy, các kết quả có thể xảy ra của phép thử trên là đồng khả năng.

⦁ Do nhân viên thuộc bộ phận Kinh doanh chiếm 55% tổng số nhân viên của công ty nên kết quả thuận lợi cho biến cố A chiếm 55% so với tổng số kết quả có thể xảy ra của phép thử, do đó xác suất của biến cố A là: $P\left(A\right)=\frac{55\%}{100\%}=\frac{11}{20}.$

⦁ Số nhân viên thuộc bộ phận Hành chính – Nhân sự và bộ phận Dịch vụ lần lượt chiếm 6% và 9% tổng số nhân viên của công ty nên kết quả thuận lợi cho biến cố B chiếm 100% – 6% – 9% = 85% so với tổng số kết quả có thể xảy ra của phép thử, do đó xác suất của biến cố B là: $P\left(B\right)=\frac{85\%}{100\%}=\frac{3}{20}.$

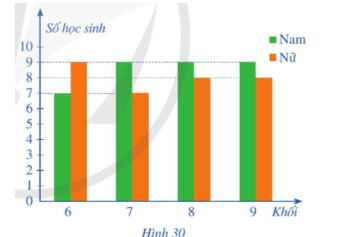
Bài 7 trang 42 Toán 9 Tập 2: Biểu đồ cột kép ở Hình 30 biểu diễn số lượng học sinh tham gia giải thi đấu thể thao của một trường trung học cơ sở.

Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó.

Tính xác suất của mỗi biến cố sau:

A: “Học sinh được chọn là nam”;

B: “Học sinh được chọn thuộc khối 6”;

C: “Học sinh được chọn là nữ và không thuộc khối 9”.

Lời giải:

Tổng số học sinh toàn trường tham gia giải đấu là:

7 + 9 + 9 + 7 + 9 + 8 + 9 + 8 = 66 (học sinh).

Xét phép thử: “Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó”.

Ta thấy, các kết quả có thể xảy ra của phép thử trên là đồng khả năng.

Tổng số học sinh nam toàn trường tham gia giải đấu là:

7 + 9 + 9 + 9 = 34 (học sinh nam).

Tổng số học sinh thuộc khối 6 tham gia giải đấu là:

7 + 9 = 16 (học sinh).

Tổng số học sinh nữ không thuộc khối 9, tức là thuộc khối 6, 7, 8 tham gia giải đấu là:

9 + 7 + 8 = 24 (học sinh).

Xác suất của biến cố A là: $P\left(A\right)=\frac{34}{66}=\frac{17}{33}.$

Xác suất của biến cố B là: $P\left(B\right)=\frac{16}{66}=\frac{8}{33}.$

Xác suất của biến cố C là: $P\left(C\right)=\frac{24}{66}=\frac{4}{11}.$

Bài 8 trang 42 Toán 9 Tập 2: Trong một kì thi học sinh giỏi Toán, tỉ lệ học sinh đạt giải là 35%. Chọn ngẫu nhiên một học sinh đã tham gia kì thi đó. Tính xác suất của biến cố: “Học sinh được chọn đạt giải”.

Lời giải:

Xác suất của biến cố: “Học sinh được chọn đạt giải” là $P=\frac{35\%}{100\%}=\frac{7}{20}.$

Lời giải bài tập Toán 9 Bài tập cuối chương 6 hay khác:

• Giải Toán 9 trang 40
• Giải Toán 9 trang 41