Bài 9.32 trang 91 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9

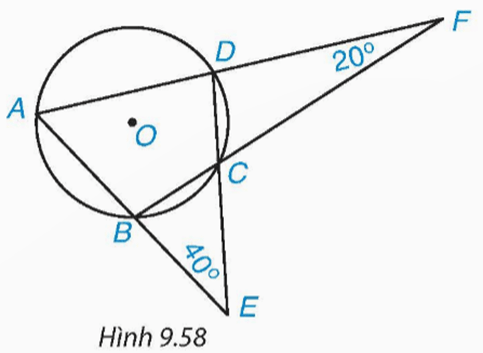
Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết và tính số đo các góc của tứ giác ABCD.

Giải Toán 9 Luyện tập chung - Kết nối tri thức

Bài 9.32 trang 91 Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết $\widehat{BEC}=40°$ và $\widehat{DFC}=20°,$ tính số đo các góc của tứ giác ABCD.

Lời giải:

Xét ∆ABF có $\hat{A}+\widehat{ABF}+\hat{F}=180°$ (tổng ba góc của tam giác)

Do đó $\widehat{ABF}=180°-\hat{F}-\hat{A}=180°-20°-\hat{A}=160°-\hat{A}.$

Xét ∆ADE có $\hat{A}+\widehat{ADE}+\hat{E}=180°$ (tổng ba góc của tam giác)

Do đó $\widehat{ADE}=180°-\hat{E}-\hat{A}=180°-40°-\hat{A}=140°-\hat{A}.$

Vì ABCD là tứ giác nội tiếp đường tròn (O) nên tổng các góc đối nhau của tứ giác bằng 180°, do đó $\hat{A}+\widehat{BCD}=180°,$ suy ra $\widehat{BCD}=180°-\hat{A}.$

Xét tứ giác ABCD có:

$\hat{A}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360°$ (tổng các góc của một tứ giác)

Suy ra $\hat{A}+\left(160°-\hat{A}\right)+\left(180°-\hat{A}\right)+\left(140°-\hat{A}\right)=360°$

Hay $2\hat{A}=120°,$ nên $\hat{A}=60°.$

Do đó $\widehat{ABC}=160°-\hat{A}=160°-60°=100°;$

$\widehat{ADC}=140°-\hat{A}=140°-60°=80°;$

$\widehat{BCD}=180°-\hat{A}=180°-60°=120°.$

Vậy tứ giác ABCD có $\hat{A}=60°;\widehat{ABC}=100°;\widehat{BCD}=120°;\widehat{ADC}=80°.$

Lời giải bài tập Toán 9 Luyện tập chung hay, chi tiết khác:

• Bài 9.31 trang 91 Toán 9 Tập 2: Cho tam giác ABC có các đường cao AD, BE, CF ....

• Bài 9.33 trang 91 Toán 9 Tập 2: Cho hình vuông ABCD có cạnh bằng 4 cm. Tính chu vi, diện tích của các đường tròn nội tiếp ....

• Bài 9.34 trang 91 Toán 9 Tập 2: Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) ....

• Bài 9.35 trang 91 Toán 9 Tập 2: Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như Hình 9.59 ....

• Bài 9.36 trang 91 Toán 9 Tập 2: Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10 cm ....