Bài 9.34 trang 91 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9

❮ Bài trước Bài sau ❯

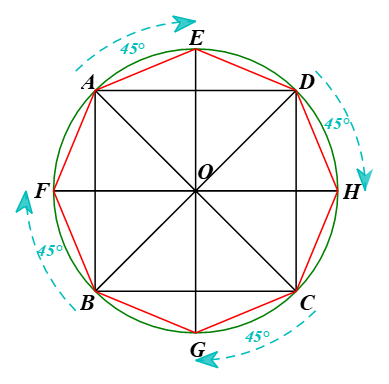
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều quay của kim đồng hồ. Phép quay thuận chiều 45° biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.

Giải Toán 9 Luyện tập chung - Kết nối tri thức

Bài 9.34 trang 91 Toán 9 Tập 2: Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều quay của kim đồng hồ. Phép quay thuận chiều 45° biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.

a) Vẽ đa giác EAFBGCHD.

b) Đa giác EAFBGCHD có phải là một bát giác đều hay không? Vì sao?

Lời giải:

Bài 9.34 trang 91 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9

⦁ Vẽ đường tròn (O). Trên đường tròn (O) vẽ hình vuông ABCD sao cho các đỉnh ABCD sao cho các đỉnh A, B, C, D theo thứ tự ngược chiều kim đồng hồ.

⦁ Lấy điểm E thuộc đường tròn (O) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OE và $\hat{A O E} = 45 ° .$

⦁ Xác định các điểm F, G, H tương tự như cách xác định điểm E ở trên. Nối A với E, E với D, D với H, H với C, C với G, G với B, B với F và F với A. Khi đó ta được đa giác EAFBGCHD.

b) Vì ABCD là hình vuông nên đường tròn (O) ngoại tiếp hình vuông có tâm O là giao điểm hai đường chéo. Do đó AC ⊥ BD tại O hay $\hat{A O D} = 90 ° .$

Suy ra $\hat{A O E} + \hat{E O D} = 90 °,$ suy ra $\hat{A O E} = 90 ° - \hat{E O D} = 90 ° - 45 ° = 45 ° .$

Xét ∆OAE và ∆OED có:

OA = OE, $\hat{A O E} = \hat{E O D}$ (cùng bằng 45°), OE = OD.

Do đó ∆OAE = ∆OED (c.g.c).

Tương tự, ta sẽ chứng minh được:

∆OAE = ∆OED = ∆ODH = ∆OHC = ∆OCG = ∆OGB = ∆OBF = ∆OFA.

Suy ra:

⦁ AE = ED = DH = HC = CG = GB = BF = FA; (1)

⦁ $\hat{O A E} = \hat{O E D} = \hat{O D H} = \hat{O H C} = \hat{O C G} = \hat{O G B} = \hat{O B F} = \hat{O F A};$

⦁ $\hat{O E A} = \hat{O D E} = \hat{O H D} = \hat{O C H} = \hat{O G C} = \hat{O B G} = \hat{O F B} = \hat{O A F} .$

Xét ∆OAE có OA = OE nên ∆OAE cân tại O, suy ra $\hat{O A E} = \hat{O E A} .$

Suy ra $\hat{O A E} + \hat{O A F} = \hat{O E D} + \hat{O E A} = \hat{O D H} + \hat{O D E} = \hat{O H C} + \hat{O H D}$

$= \hat{O C G} + \hat{O C H} = \hat{O G B} + \hat{O G C} = \hat{O B F} + \hat{O B G} = \hat{O F A} + \hat{O F B} .$

Hay $\hat{E A F} = \hat{A F B} = \hat{F B G} = \hat{B G C} = \hat{G C H} = \hat{C H D} = \hat{H D E} = \hat{D E A} . (2)$

Từ (1) và (2) suy ra EAFBGCHD có các cạnh bằng nhau và các góc bằng nhau.

Vậy EAFBGCHD là bát giác đều.

Lời giải bài tập Toán 9 Luyện tập chung hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯