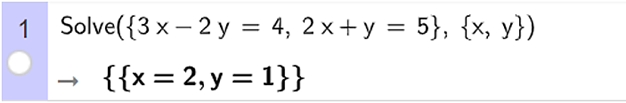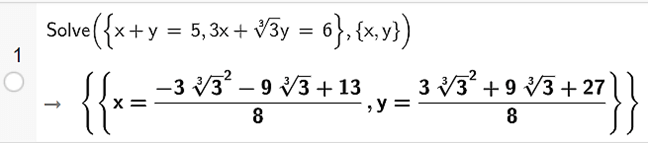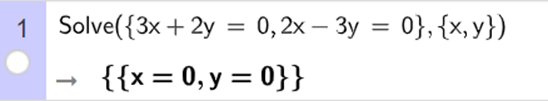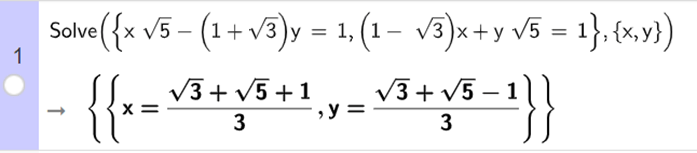Thực hành 2 trang 114 Toán 9 Tập 2 | Kết nối tri thức Giải Toán 9

---

Giải các hệ phương trình sau:

Giải Toán 9 Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra - Kết nối tri thức

Thực hành 2 trang 114 Toán 9 Tập 2: Giải các hệ phương trình sau:

a) $\left\{\begin{array}{l}3x-2y=4\\ 2x+y=5;\end{array}\right.$

b) $\left\{\begin{array}{l}x+y=5\\ 3x+\sqrt[3]{3}y=6;\end{array}\right.$

c) $\left\{\begin{array}{l}3x+2y=0\\ 2x-3y=0;\end{array}\right.$

d) $\left\{\begin{array}{l}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\\ \left(1-\sqrt{3}\right)x+y\sqrt{5}=1.\end{array}\right.$

Lời giải:

Bước 1. Khởi động phần mềm Geogebrra , chọn Complex Adaptive System (CAS).

Bước 2.

Cách 1: Ta dùng lệnh Solve ({<phương trình thứ nhất>, <phương trình thứ hai>}), {<biến số thứ nhất>, <biến số thứ hai>}), hoặc Solitions ({<phương trình thứ nhất>, <phương trình thứ hai>}), {<biến số thứ nhất>, <biến số thứ hai>}) trên ô lệnh của cửa sổ CAS để giải hệ phương trình.

Cách 2: Sử dụng câu lệnh Intersect ({<phương trình thứ nhất>, (<phương trình thứ hai>}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.

a) $\left\{\begin{array}{l}3x-2y=4\\ 2x+y=5\end{array}\right.$

Ta nhập Solve ({3x – 2y = 4, 2x + y = 5}, {x, y}), ta thu được kết quả như hình vẽ.

Vậy hệ phương trình đã cho có nghiệm là x = 2; y = 1.

b) $\left\{\begin{array}{l}x+y=5\\ 3x+\sqrt[3]{3}y=6\end{array}\right.$

Ta nhập Solve ({x + y = 5, 3x + cbrt(3)y = 6}, {x, y}), ta thu được kết quả như hình vẽ.

Vậy hệ phương trình đã cho có nghiệm là $x=\frac{-3{\sqrt[3]{3}}^2-9\sqrt[3]{3}+13}{8};y=\frac{3{\sqrt[3]{3}}^2+9\sqrt[3]{3}+27}{8}.$

c) $\left\{\begin{array}{l}3x+2y=0\\ 2x-3y=0\end{array}\right.$

Ta nhập Solve ({3x + 2y = 0, 2x – 3y = 0}, {x, y}), ta thu được kết quả như hình vẽ.

Vậy hệ phương trình đã cho có nghiệm là x = 0; y = 0.

c) $\left\{\begin{array}{l}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\\ \left(1-\sqrt{3}\right)x+y\sqrt{5}=1\end{array}\right.$

Ta nhập Solve ({x sqrt(5) – (1 + sqrt(3))y = 1, (1 – sqrt(3))x – y sqrt(5) = 1}, {x, y}), ta thu được kết quả như hình vẽ.

Vậy hệ phương trình đã cho có nghiệm là $x=\frac{\sqrt{3}+\sqrt{5}+1}{3};y=\frac{\sqrt{3}+\sqrt{5}-1}{3}.$

Lời giải bài tập Toán 9 Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra hay, chi tiết khác:

• Thực hành 1 trang 114 Toán 9 Tập 2: Giải các phương trình sau: a) x2 – 4x + 10 = 0; ....

• Thực hành 3 trang 114 Toán 9 Tập 2: Cho đường thẳng (d): y = 2x + $\sqrt{3}$ và parabol (P): y = x² ....