Giải Toán 9 trang 71 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 71 Tập 2 trong Bài 27: Góc nội tiếp Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 71.

Giải Toán 9 trang 71 Tập 2 Kết nối tri thức

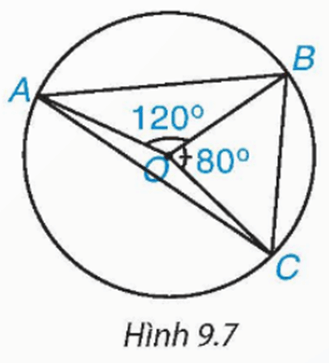
Bài 9.2 trang 71 Toán 9 Tập 2: Cho các điểm như Hình 9.7. Tính số đo các góc của tam giác ABC, biết rằng $\widehat{AOB}=120°,$ $\widehat{BOC}=80°.$

Lời giải:

Xét đường tròn (O) có:

⦁ $\widehat{BAC},\widehat{BOC}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ BC, nên $\widehat{BAC}=\frac{1}{2}\widehat{BOC}=\frac{1}{2}\cdot 80°=40°;$

⦁ $\widehat{ACB},\widehat{AOB}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ AB, nên $\widehat{ACB}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}\cdot 120°=60°.$

Xét ∆ABC có: $\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180°$ (định lí tổng các góc của một tam giác)

Suy ra $\widehat{ABC}=180°-\widehat{ACB}-\widehat{BAC}=180°-60°-40°=80°.$

Vậy $\widehat{ABC}=80°,\widehat{BAC}=40°;\widehat{ACB}=60°.$

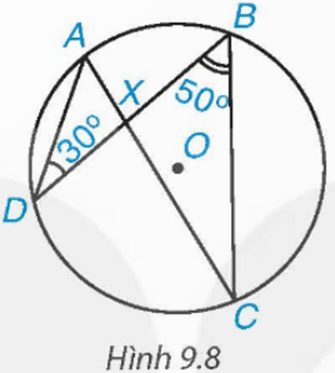
Bài 9.3 trang 71 Toán 9 Tập 2: Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X (H.9.8). Tính số đo góc AXB biết rằng $\widehat{ADB}=30°$ và $\widehat{DBC}=50°.$

Lời giải:

Xét đường tròn (O) có $\widehat{ADB},\widehat{ACB}$ là hai góc nội tiếp cùng chắn cung nhỏ AB nên $\widehat{ACB}=\widehat{ADB}=30°.$

Vì $\widehat{AXB}$ là góc ngoài của ∆BXC tại đỉnh X nên ta có:

$\widehat{AXB}=\widehat{XCB}+\widehat{XBC}=30°+50°=80°.$

Vậy $\widehat{AXB}=80°.$

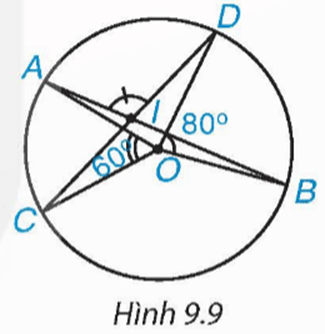
Bài 9.4 trang 71 Toán 9 Tập 2: Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) (H.9.9).

a) Biết rằng $\widehat{AOC}=60°,$ $\widehat{BOD}=80°.$ Tính số đo của góc AID.

b) Chứng minh rằng IA . IB = IC . ID.

Lời giải:

a) Xét đường tròn (O) có:

⦁ $\widehat{BAD},\widehat{BOD}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ BD, nên $\widehat{BAD}=\frac{1}{2}\widehat{BOD}=\frac{1}{2}\cdot 80°=40°.$

⦁ Vì $\widehat{ADC},\widehat{AOC}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ AC, nên $\widehat{ADC}=\frac{1}{2}\widehat{AOC}=\frac{1}{2}\cdot 60°=30°.$

Xét ∆AID có: $\widehat{AID}+\widehat{DAI}+\widehat{ADI}=180°$ (định lí tổng các góc của một tam giác)

Suy ra $\widehat{AID}=180°-\widehat{DAI}-\widehat{ADI}=180°-40°-30°=110°.$

Vậy $\widehat{AID}=110°.$

b) Xét đường tròn (O) có $\widehat{ADC}$ và $\widehat{ABC}$ là hai góc nội tiếp cùng chắn cung nhỏ AC nên $\widehat{ADC}=\widehat{ABC}$ hay $\widehat{ADI}=\widehat{CBI}.$

Xét ∆AID và ∆CIB có:

$\widehat{AID}=\widehat{CIB}$ (hai góc đối đỉnh);

$\widehat{ADI}=\widehat{CBI}$ (chứng minh trên).

Do đó ∆AID ᔕ ∆CIB (g.g).

Suy ra $\frac{IA}{IC}=\frac{ID}{IB}$ (tỉ số các cạnh tương ứng) hay IA . IB = IC . ID.

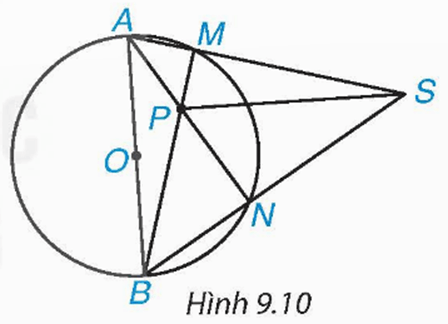
Bài 9.5 trang 71 Toán 9 Tập 2: Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A) và N (khác B). Gọi P là giao điểm của BM và AN (H.9.10). Chứng minh rằng SP vuông góc với AB.

Lời giải:

Xét đường tròn (O) có: $\widehat{AMB}$ và $\widehat{ANB}$ đều là góc nội tiếp cùng chắn nửa đường tròn nên $\widehat{AMB}=90°$ và $\widehat{ANB}=90°.$

Suy ra BM ⊥ AM và AN ⊥ BN

Hay BM ⊥ AS và AN ⊥ BS.

Xét ∆ABS có AN, BM là hai đường cao (BM ⊥ AS và AN ⊥ BS) cắt nhau tại P nên P là trực tâm của ∆ABS, suy ra SP ⊥ AB.

Vậy SP ⊥ AB.

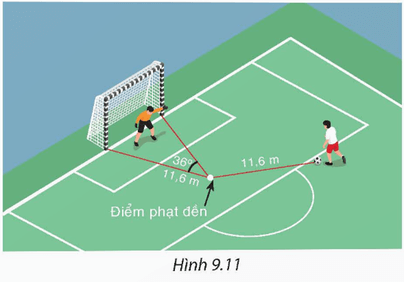
Bài 9.6 trang 71 Toán 9 Tập 2: Trên sân bóng, khi quả bóng được đặt tại điểm phạt đền thì có góc sút bằng 36° và quả bóng cách mỗi cọc gôn 11,6 m (H.9.11). Hỏi khi quả bóng đặt ở vị trí cách điểm phạt đến 11,6 m thì góc sút bằng bao nhiêu?

Lời giải:

Hình vẽ dưới đây minh họa cho bài toán trên với A, B lần lượt là các cọc gôn, C là vị trí đặt bóng và O là vị trí điểm phạt đền.

Vì OA = OB = OC = 11,6 m nên A, B, C cùng thuộc đường tròn (O; 11,6 m).

Xét đường tròn (O; 11,6 m) có $\widehat{ACB},\widehat{AOB}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ AB nên $\widehat{ACB}=\frac{1}{2}\cdot \widehat{AOB}=\frac{1}{2}\cdot 36°=18°.$

Vậy khi quả bóng đặt ở vị trí cách điểm phạt đến 11,6 m thì góc sút bằng 18°.

Lời giải bài tập Toán 9 Bài 27: Góc nội tiếp hay khác:

• Giải Toán 9 trang 70