Giải Toán 9 trang 82 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 82 Tập 2 trong Bài 29: Tứ giác nội tiếp Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 82.

Giải Toán 9 trang 82 Tập 2 Kết nối tri thức

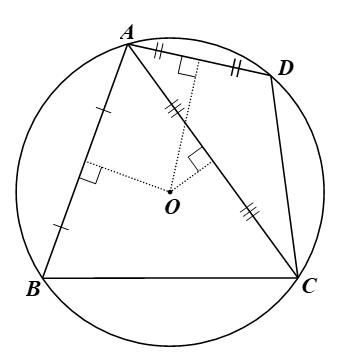
Thử thách nhỏ 1 trang 82 Toán 9 Tập 2: Cho tứ giác ABCD, biết rằng các đường trung trực của ba đoạn thẳng AB, AC, AD đồng quy tại một điểm. Hãy giải thích vì sao ABCD là tứ giác nội tiếp.

Lời giải:

Gọi O là giao điểm của các đường trung trực của ba đoạn thẳng AB, AC, AD.

Vì O nằm trên đường trung trực của AB nên OA = OB.

Vì O nằm trên đường trung trực của AC nên OA = OC.

Vì O nằm trên đường trung trực của AD nên OA = OD.

Do đó OA = OB = OC = OD.

Suy ra bốn điểm A, B, C, D đều nằm trên đường tròn (O).

Vậy ABCD là tứ giác nội tiếp.

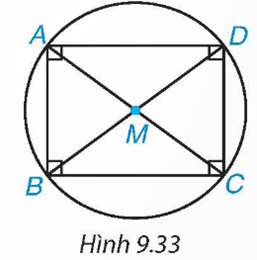
HĐ4 trang 82 Toán 9 Tập 2: Vẽ hình chữ nhật ABCD và giao điểm M của hai đường chéo AC và BD (H.9.33).

a) Hãy giải thích vì sao điểm M cách đều bốn đỉnh của hình chữ nhật ABCD.

b) Chứng tỏ rằng hình chữ nhật ABCD nội tiếp một đường tròn có bán kính bằng nửa đường chéo hình chữ nhật.

Lời giải:

a) Hình chữ nhật ABCD có M là giao điểm của hai đường chéo AC và BD nên:

⦁ AC = BD;

⦁ M là trung điểm của AC và BD, suy ra MA = MC = $\frac{1}{2}$AC; MB = MD = $\frac{1}{2}$BD.

Do đó MA = MB = MC = MD = $\frac{1}{2}$AC = $\frac{1}{2}$BD.

Vậy điểm M cách đều bốn đỉnh của hình chữ nhật ABCD.

b) Theo câu a, MA = MB = MC = MD = $\frac{1}{2}$AC = $\frac{1}{2}$BD nên bốn điểm A, B, C, D cùng nằm trên đường tròn tâm M, bán kính bằng $\frac{1}{2}$AC.

Vậy hình chữ nhật ABCD nội tiếp đường tròn tâm M là giao điểm hai đường chéo, bán kính bằng nửa đường chéo hình chữ nhật.

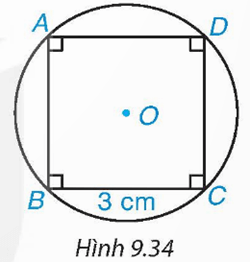
HĐ5 trang 82 Toán 9 Tập 2: Cho hình vuông ABCD có cạnh bằng 3 cm (H.9.34). Hãy xác định tâm, vẽ đường tròn ngoại tiếp hình vuông ABCD và cho biết bán kính của đường tròn đó.

Lời giải:

Gọi O là giao điểm hai đường chéo AC và BD của hình vuông.

Vì ABCD là hình vuông nên OA = OB = OC = OD = $\frac{1}{2}$AC = $\frac{1}{2}$BD.

Do đó bốn điểm A, B, C, D cùng nằm trên đường tròn tâm O, bán kính bằng nửa đường chéo AC.

Xét ∆ABC vuông tại B (do ABCD là hình vuông nên $\hat{B}=90°)$ có:

AC² = AB² + BC² = 3² + 3² = 18.

Suy ra $AC=\sqrt{18}=3\sqrt{2}\text{(cm).}$

Do đó OA = OB = OC = OD = $\frac{1}{2}$.3$\sqrt{2}$ = $\frac{3\sqrt{2}}{2}$ (cm)

Vậy đường tròn ngoại tiếp hình vuông ABCD có tâm là giao điểm hai đường chéo và bán kính bằng $\frac{3\sqrt{2}}{2}$ cm.

Câu hỏi trang 82 Toán 9 Tập 2: Với điểm A cho trước nằm trên đường tròn (O), có bao nhiêu hình vuông có một đỉnh là A nội tiếp đường tròn (O)?

Lời giải:

Ta đã biết, một hình vuông luôn có một đường tròn ngoại tiếp có tâm là giao điểm hai đường chéo và bán kính bằng nửa độ dài đường chéo hình vuông.

Giả sử dựng được hình vuông ABCD nội tiếp đường tròn (O). Lúc này, đường chéo AC là đường kính của (O).

Mặt khác, hình vuông ABCD có đường chéo AC là đường phân giác của góc BAD nên $\widehat{BAC}=\widehat{DAC}=\frac{1}{2}\widehat{BAD}=\frac{1}{2}\cdot 90°=45°.$

Do đó, từ một điểm A cho trước nằm trên đường tròn (O), ta xác định được duy nhất một đường kính AC. Khi đó, ta cũng xác định được duy nhất một điểm B và một điểm D cùng nằm trên đường tròn (O) thỏa mãn $\widehat{BAC}=\widehat{DAC}=45°.$

Vậy với điểm A cho trước nằm trên đường tròn (O), có duy nhất một hình vuông có một đỉnh là A nội tiếp đường tròn (O).

Lời giải bài tập Toán 9 Bài 29: Tứ giác nội tiếp hay khác:

• Giải Toán 9 trang 80

• Giải Toán 9 trang 81

• Giải Toán 9 trang 83