Giải Toán 9 trang 87 Tập 2 Kết nối tri thức
Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 87 Tập 2 trong Bài 30: Đa giác đều Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 87.
Giải Toán 9 trang 87 Tập 2 Kết nối tri thức
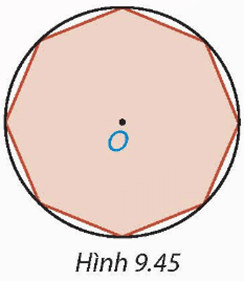
Thử thách nhỏ 1 trang 87 Toán 9 Tập 2: Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?
Lời giải:
Cách 1:
Giả sử ABCDEGHK là bát giác đều nội tiếp đường tròn (O).
Do đó AB = BC = CD = DE = EG = GH = HK và OA = OB = OC = OD = OE = OG = OH = OK.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC
Do đó ∆OAB = ∆OBC (c.c.c).
Tương tự, ta sẽ chứng minh được:
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOG = ∆GOH = ∆HOK = ∆KOA.
Suy ra các góc tương ứng bằng nhau:
Ta có:
Suy ra nên
Lại có (tổng ba góc của ∆OAB bằng 180°)
Suy ra
Vì ∆AOB = ∆OKA nên (hai góc tương ứng).
Suy ra
Do đó, vì ABCDEGHK là bát giác đều nên các góc bằng nhau và bằng 135°.
Cách 2:
Bát giác đều ABCDEGHK được chia thành ba tứ giác ABCD, ADEG và AGHG.
Ta thấy tổng số đo các góc của bát giác ABCDEGHK bằng tổng số đo các góc của ba tứ giác kể trên.
Mà mỗi tứ giác có tổng số đo các góc bằng 360°, do đó tổng số đo các góc của bát giác đều ABCDEGHK là: 3.360° = 1 080°.
Vì ABCDEGHK là bát giác đều nên 8 góc của bát giác bằng nhau và mỗi góc có số đo bằng
Vậy mỗi góc của bát giác đều có số đo bằng 135°.
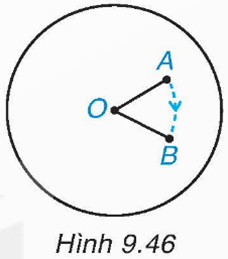
HĐ2 trang 87 Toán 9 Tập 2: Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có dạng hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay có dạng hình tròn với tâm O sao cho điểm A khác điểm O. Khi quay bàn xoay thuận chiều quay của kim đồng hồ (H.9.46) thì chiếc cốc di chuyển đến một vị trí mới là điểm B.
Em hãy so sánh khoảng cách từ hai điểm A và B đến điểm O. Hai điểm A, B có cùng nằm trên một đường tròn tâm O hay không?
Lời giải:
Khi quay bàn xoay thì khoảng cách từ tâm O đến chiếc cốc không thay đổi nên OA = OB. Do đó khoảng cách từ hai điểm A và B đến điểm O bằng nhau.
Vì OA = OB nên hai điểm A, B cùng nằm trên đường tròn tâm O.
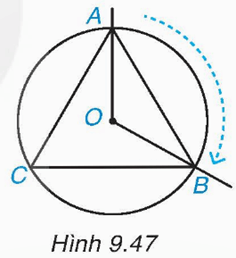
HĐ3 trang 87 Toán 9 Tập 2: Trên bàn xoay tâm O, vẽ tam giác đều ABC nội tiếp một đường tròn (O) và hai tia OA, OB (H.9.47). Khi quay bàn xoay thuận chiều quay của kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), điểm A có di chuyển đến vị trí của điểm B không và sẽ di chuyển trên cung tròn nào của đường tròn (O)? Khi đó, điểm C sẽ di chuyển đến vị trí của điểm nào?
Lời giải:
Vì tam giác ABC đều nên AB = BC = CA.
Vì tam giác ABC nội tiếp đường tròn (O) nên OA = OB = OC.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC
Do đó ∆OAB = ∆OBC (c.c.c)
Suy ra (hai góc tương ứng).
Vì vậy, nếu quay bàn xoay thuận chiều quay của kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), điểm A di chuyển đến vị trí của điểm B và sẽ di chuyển trên cung tròn AB của đường tròn (O).
Khi đó, tia OB di chuyển trùng với tia OC (ở vị trí ban đầu), tia OC di chuyển trùng với tia OA (ở vị trí ban đầu). Vậy điểm C sẽ di chuyển đến vị trí của điểm A.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay khác: