Giải Toán 9 trang 89 Tập 2 Kết nối tri thức
Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 89 Tập 2 trong Bài 30: Đa giác đều Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 89.
Giải Toán 9 trang 89 Tập 2 Kết nối tri thức
Thử thách nhỏ 2 trang 89 Toán 9 Tập 2: Hãy liệt kê 6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O).
Lời giải:
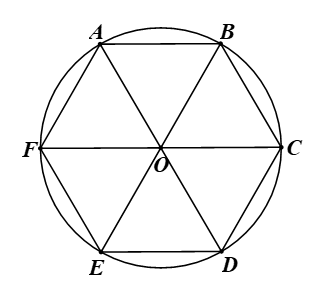
Giả sử lục giác đều ABCDEF nội tiếp đường tròn (O) (hình vẽ).
Vì lục giác ABCDEF nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE = OF.
Vì ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC.
Do đó ∆OAB = ∆OBC (c.c.c).
Chứng minh tương tự ta có
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOF = ∆FOA.
Suy ra
Mà
Do đó
Suy ra
Khi đó phép quay ngược chiều 72° tâm O giữ nguyên điểm O, biến điểm A thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB, điểm A tạo nên cung AB có số đo 60°.
Vậy mỗi phép quay thuận chiều 60° tâm O ở mỗi đỉnh A, B, C, D, E, F sẽ giữ nguyên lục giác đều nội tiếp đường tròn tâm O.
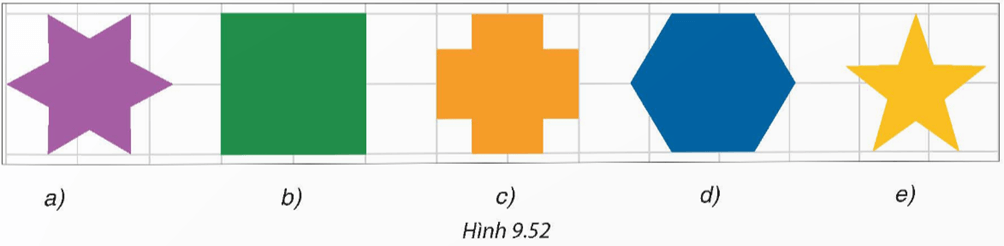
Bài 9.24 trang 89 Toán 9 Tập 2: Trong các hình phẳng sau (H.9.52), hình nào là hình phẳng có dạng đa giác đều?
Lời giải:
Hình b là hình vuông, hình d là hình lục giác đều vì hai hình đều có các cạnh bằng nhau và các góc bằng nhau.
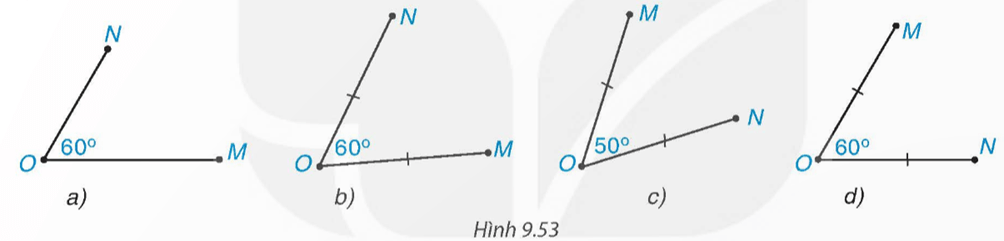
Bài 9.25 trang 89 Toán 9 Tập 2: Trong các hình dưới đây (H.9.53), hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều 60° tâm O biến điểm M thành điểm N?
Lời giải:
Phép quay thuận chiều 60° tâm O biến điểm M thành điểm N tức là điểm N thuộc đường tròn (O; OM) sao cho tia OM quay thuận kim đồng hồ đến tia ON và điểm M tạo nên cung MN có số đo là 60°.
Trong các hình đã cho, hình d là hình cần tìm.
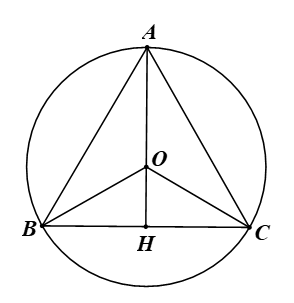
Bài 9.26 trang 89 Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm. Tính độ dài các cạnh của tam giác ABC.
Lời giải:
Vì tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm nên ta có OA = OB = OC = 2 cm.
Vì ABC là tam giác đều nên tâm O của đường tròn ngoại tiếp tam giác là trọng tâm của tam giác.
Gọi H là giao điểm của AO và BC. Khi đó AH vừa là đường trung trực, vừa đường cao, vừa là đường trung tuyến của tam giác.
Do đó suy ra
Vì ∆ABC đều nên
Xét ∆ABH vuông tại H, ta có:
Vì AH là đường trung tuyến của ∆ABC nên H là trung điểm của BC, do đó BC = 2BH = 2 (cm)
Vậy các cạnh của tam giác ABC có độ dài bằng 2 cm.
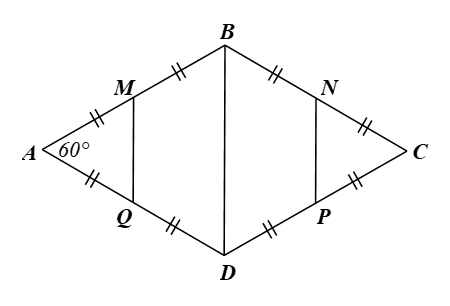
Bài 9.27 trang 89 Toán 9 Tập 2: Cho hình thoi ABCD có Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Lời giải:
⦁ Vì ABCD là hình thoi nên AB = BC = CD = DA.
Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên MA = MB = AB; NB = NC = BC; PC = PD = CD; QD = QA = DA.
Do đó AM = MB = NB = NC = PC = PD = QD = QA = AB. (1)
Xét ∆ABD có AB = AD nên ∆ABD cân tại A, lại có nên ∆ABD là tam giác đều. Do đó AB = BD (2) và
Lại có M, Q là lần lượt là trung điểm của AB, AD nên MQ là đường trung bình của tam giác. Do đó MQ // BD và MQ = BD. (3)
Chứng minh tương tự, ta cũng có NP = BD. (4)
Từ (1), (2), (3) và (4) suy ra MB = BN = NP = PD = DQ = QM.
⦁ Vì MQ // BD nên (so le trong).
Mà (hai góc kề bù)
Suy ra
Tương tự, ta có
Tam giác BCD có BC = CD và (tính chất hình thoi) nên ∆BCD là tam giác đều. Do đó
Ta có
Khi đó,
Như vậy MBNPDQ có các cạnh bằng nhau và các góc bằng nhau.
Vậy MBNPDQ là lục giác đều.
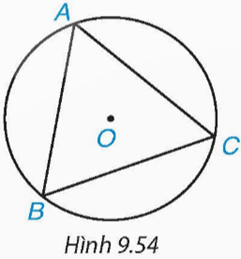
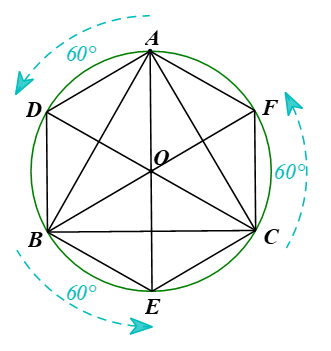
Bài 9.28 trang 89 Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn (O) như Hình 9.54. Phép quay ngược chiều 60° tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.
Lời giải:
⦁ Vì ∆ABC là tam giác đều nên
Xét đường tròn (O) có lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AB nên suy ra
⦁ Vì phép quay ngược chiều 60° tâm O biến điểm A thành các điểm D nên điểm D nằm trên đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OD thì điểm A tạo nên cung AD có số đo 60°.
Khi đó ta có OA = OD và nên ∆OAD là tam giác đều.
Suy ra AD = OA = OD và
⦁ Mặt khác, (hai góc kề nhau)
Nên
Xét ∆BOD có OB = OD (cùng bằng OA) và nên ∆BOD là tam giác đều.
Do đó BD = OB = OD và
Từ (1) và (2) ta có AD = DB và
Tương tự, ta sẽ chứng minh được:
AD = DB = BE = EC = CF = FA và
Vậy ADBECF có các cạnh bằng nhau và các góc đều bằng 120° nên là một lục giác đều.
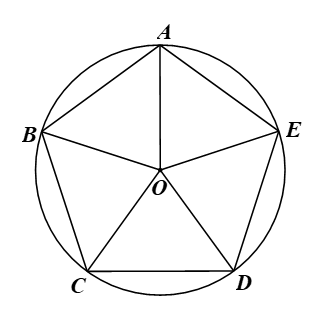
Bài 9.29 trang 89 Toán 9 Tập 2: Liệt kê năm phép quay giữ nguyên một ngũ giác đều nội tiếp một đường tròn tâm O.
Lời giải:
Giả sử ABCDE là ngũ giác đều nội tiếp đường tròn (O) (hình vẽ).
Vì ngũ giác ABCDE nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE.
Vì ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC.
Do đó ∆OAB = ∆OBC (c.c.c).
Chứng minh tương tự ta có
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOA.
Suy ra
Mà
Do đó
Suy ra
Khi đó phép quay ngược chiều 72° tâm O giữ nguyên điểm O, biến điểm A thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB, điểm A tạo nên cung AB có số đo 72°.
Vậy mỗi phép quay ngược chiều 72° tâm O ở mỗi đỉnh A, B, C, D, E sẽ giữ nguyên ngũ giác đều nội tiếp một đường tròn tâm O.
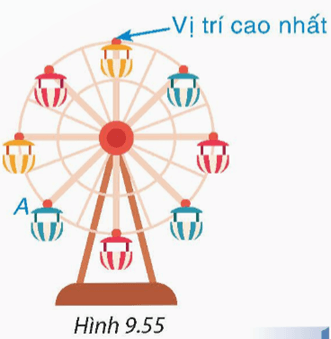
Bài 9.30 trang 89 Toán 9 Tập 2: Cho vòng quay mặt trời gồm tám cabin như Hình 9.55. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều quay của kim đồng hồ quanh tâm bao nhiêu độ?
Lời giải:
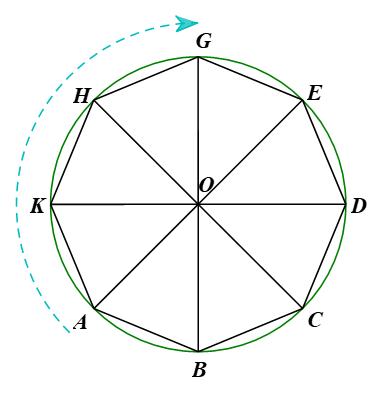
Giả sử 8 cabin tạo thành một bát giác đều ABCDEGHK nội tiếp đường tròn (O) (hình vẽ).
Vì bát giác ABCDEGHK nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE = OG = OH = OK.
Vì ABCDEGHK là ngũ giác đều nên AB = BC = CD = DE = EG = GH = HK = KA.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC.
Do đó ∆OAB = ∆OBC (c.c.c).
Chứng minh tương tự ta có
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOG = ∆GOH = ∆HOK = ∆KOA.
Suy ra
Mà
Do đó
Suy ra
Khi đó
Để cabin A di chuyển đến vị trí cao nhất (vị trí của cabin G ban đầu) thì tia OA quay thuận chiều kim đồng hồ đến tia OG, điểm A tạo nên cung AG có số đo 135°.
Vậy để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm có số đo là 135°.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay khác: