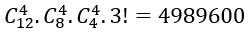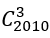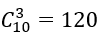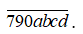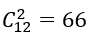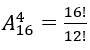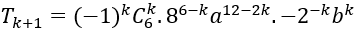60 bài tập trắc nghiệm Tổ hợp chọn lọc, có lời giải - Toán lớp 11
60 bài tập trắc nghiệm Tổ hợp chọn lọc, có lời giải
Với 60 bài tập trắc nghiệm Tổ hợp chọn lọc, có lời giải Toán lớp 11 tổng hợp 60 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tổ hợp từ đó đạt điểm cao trong bài thi môn Toán lớp 11.
Bài 1: Trong khai triển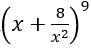 
, số hạng không chứa x là:
A. 4308. B. 86016. C. 84. D. 43008.
Lời giải:
Đáp án: D
Chọn D.
Bài 2: Nếu Ax2=110 thì:
A. x=10. B. x=11. C. x=11 hay x=10. D. x=0
Lời giải:
Đáp án: B
Chọn B.
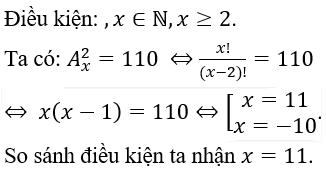
Bài 3: Xếp 6 người A, B, C, D, E, F vào một ghế dài.Hỏi có bao nhiêu cách sắp xếp sao cho: A và F ngồi cạnh nhau
A. 242 B. 240 C. 244 D. 248
Lời giải:
Đáp án: B
Xem AF là một phần tử X, ta có: 5! = 120 số cách xếp X,B,C,D, E. Khi hoán vị A,F ta có thêm được một cách xếp
Vậy có 240 cách xếp thỏa yêu cầu bài toán. Chọn B.
Bài 4: Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố C đến thành phố B và muốn đi từ thành phố A đến thành phố D bắt buộc phải đi qua B hoặc C. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.
A.6. B. 12. C. 18. D. 36.
Lời giải:
Đáp án: B
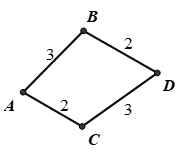
Số cách đi từ A đến D bằng cách đi từ A đến B rồi đến D là 3.2 = 6.
Số cách đi từ A đến D bằng cách đi từ A đến C rồi đến D là 2.3 = 6.
Nên có: 6 + 6 = 12 cách. Chọn B
Bài 5: Từ các số 0,1,2,3,4,5 có thể lập được:
Bao nhiêu số có ba chữ số ( không nhất thiết khác nhau) và là số chẵn?
A.60 B.90 C.450 D.100
Lời giải:
Đáp án: B
Gọi tập hợp E = {0,1,2,3,4,5}
Số tự nhiên có 3 chữ số có dạng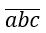 
(a ≠ 0,a,b,c ∈ E)
Vì 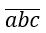là số chẵn nên c ∈ {0,2,4} từ đó ta có ba cách chọn chữ số c ( vì c ∈ {0,2,4}).
Ứng với mỗi cách chọn c ta có 6 cách chọn chữ số b (vì b ∈ E)
ứng với mỗi cách chọn c, b ta có 5 cách chọn chữ số a (vì a ∈ E và a ≠ 0)
Áp dụng quy tắc nhân ta có 3.6.5 = 90 số có 3 chữ số. Vì vậy đáp án là B.
Bài 6: Một liên đoàn bóng đá có 10 đội, mỗi đội phải đá 4 trận với mỗi đội khác, 2 trận ở sân nhà và 2 trận ở sân khách. Số trận đấu được sắp xếp là:
A. 180 B. 160. C. 90. D. 45.
Lời giải:
Đáp án: A
Mỗi đội sẽ gặp 9 đội khác trong hai lượt trận sân nhà và sân khách. Có 10.9 = 90 trận.
Mỗi đội đá 2 trận sân nhà, 2 trận sân khách. Nên số trận đấu là 2.90 = 180 trận. Chọn A
Bài 7: Có bao nhiêu tam giác mà ba đỉnh của nó thuộc vào 2010 điểm đã cho.
A. 141427544 B. 1284761260 C. 1351414120 D. 453358292
Lời giải:
Đáp án: C
Mỗi tam giác thỏa yêu cầu bài toán ứng với một tổ hợp chập 3 của 2010, nên số tam giác cần tìm là: 
Bài 8: Xếp 6 người A, B, C, D, E, F vào một ghế dài.Hỏi có bao nhiêu cách sắp xếp sao cho: A và F không ngồi cạnh nhau
A. 480 B. 460 C. 246 D. 260
Lời giải:
Đáp án: A
Ta có: 6! = 720 số cách xếp A,B,C,D, E,F. Dựa vào bài 1 số cách để A và F ngồi cạnh nhau là 240. Vậy số cách để A, F không ngồi cạnh nhau là: 720 – 240 = 480 cách. Chọn A.
Bài 9: Có 10 cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người phụ nữ trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng:
A. 100. B. 91. C.10. D.90.
Lời giải:
Đáp án: D
Có 10 cách chọn 1 người đàn ông.
Có 10 cách chọn 1 người phụ nữ.
Có 10 cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho hai người đó là vợ chồng
Tổng số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng: 10.10 – 10 = 90
Nên chọn D.
Bài 10: Cho các số 1,5,6,7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số với các chữ số khác nhau:
A. 12. B. 24. C. 64. D. 256.
Lời giải:
Đáp án: B
Gọi số tự nhiên có 4 chữ số cần tìm là: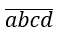 
(a ≠ 0,a,b,c,d ∈ {1,5,6,7}), khi đó:
a có 4 cách chọn
b có 3 cách chọn
c có 2 cách chọn
d có 1 cách chọn
Vậy có: 4.3.2.1 = 24 số
Nên chọn B.
Bài 11: Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:
Lời giải:
Đáp án: A
Chọn 3 trong 5 màu để tô vào 3 nước khác nhau nên có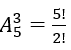 
cách. Chọn A.
Bài 12: Số tam giác xác định bởi các đỉnh của một đa giác đều 10 cạnh là:
A. 35. B.120. C.240. D.720.
Lời giải:
Đáp án: B
Chọn B.
Cứ ba đỉnh của đa giác sẽ tạo thành một tam giác.
Chọn 3 trong 10 đỉnh của đa giác, có 
Vậy có 120 tam giác xác định bởi các đỉnh của đa giác 10 cạnh.
Bài 13: Có bao nhiêu cách xếp n người ngồi vào một bàn tròn.
A. n! B. (n – 1)! C. 2(n – 1)! D. (n – 2)!
Lời giải:
Đáp án: B
Nếu xếp một người ngồi vào một vị trí nào đó thì ta có 1 cách xếp và n – 1 người còn lại được xếp vào n - 1 vị trí còn lại nên có (n – 1)! cách xếp.
Vậy có tất cả (n – 1)! cách xếp. Chọn B.
Bài 14: Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có 8 màu khác nhau, các cây bút chì cũng có 8 màu khác nhau. Như vậy bạn có bao nhiêu cách chọn
A.64. B. 16. C. 32. D.20.
Lời giải:
Đáp án: A
Chọn cây bút mực : có 8 cách
Chọn cây bút chì : có 8 cách
Theo quy tắc nhân, số cách mua là : 8.8 = 64 (cách). Chọn A
Bài 15: Từ các chữ số 2,3,5,4 có thể lập được bao nhiêu số gồm 4 chữ số:
A. 256. B. 120. C. 24. D. 16.
Lời giải:
Đáp án: A
Gọi số tự nhiên có 4 chữ số cần tìm là: 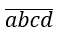(a ≠ 0,a,b,c,d ∈ {2,3,5,4}, khi đó:
a có 4 cách chọn
b có 4 cách chọn
c có 4 cách chọn
d có 4 cách chọn
Vậy có: 4.4.4.4 = 256 số
Nên chọn A.
Bài 16: Tên 15 học sinh được ghi vào 15 tờ giấy để vào trong hộp. Chọn tên 4 học sinh để cho đi du lịch. Hỏi có bao nhiêu cách chọn các học sinh:
A. 4!. B.15!. C.1365. D.32760.
Lời giải:
Đáp án: C
Chọn 4 trong 15 học sinh (không phân biệt thứ tự) là tổ hợp chập 4 của 15.
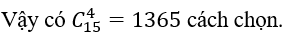
Bài 17: Nếu tất cả các đường chéo của đa giác đều 12 cạnh được vẽ thì số đường chéo là:
A.121. B.66. C. 132. D.54.
Lời giải:
Đáp án: D
Chọn D.
Cứ 2 đỉnh của đa giác sẽ tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
Khi đó có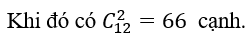 
cạnh.
Số đường chéo là: 66 – 12 = 54.
Bài 18: Cho các số 1,2,4,5,7 có bao nhiêu cách tạo ra một số chẵn gồm 3 chữ số khác nhau từ 5 chữ số đã cho:
A. 120. B.256. C.24. D.36.
Lời giải:
Đáp án: C
Bài 19: Trong một tuần, bạn A dự định mỗi ngày đi thăm một người bạn trong 12 người bạn của mình. Hỏi bạn A có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình (Có thể thăm một bạn nhiều lần).
A. 7!. B. 35831808. C. 12!. D.3991680.
Lời giải:
Đáp án: B
Thứ 2 : có 12 cách chọn bạn đi thăm
Thứ 3 : có 12 cách chọn bạn đi thăm
Thứ 4 : có 12 cách chọn bạn đi thăm
Thứ 5 : có 12 cách chọn bạn đi thăm
Thứ 6 : có 12 cách chọn bạn đi thăm
Thứ 7 : có 12 cách chọn bạn đi thăm
Chủ nhật : có 12 cách chọn bạn đi thăm
Vậy theo quy tắc nhân, có 127 = 35831808 (kế hoạch). Chọn B.
Bài 20: Có bao nhiêu chữ số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số 0,1,2,4,5,6,8.
A. 252 B. 520 C. 480 D. 368
Lời giải:
Đáp án: B
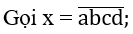
a,b,c,d ∈ {0,1,2,4,5,6,8},a ≠ 0.
Vì x là số chẵn nên d ∈ {0,2,4,6,8}.
TH1: d = 0 ⇒ có 1 cách chọn d.
Vì a ≠ 0 nên ta có 6 cách chọn a ∈ {1,2,4,5,6,8}.
Với mỗi cách chọn a, d ta có 5 cách chọn b ∈ {1,2,4,5,6,8}\{a}.
Với mỗi cách chọn a, b, d ta có 4 cách chọn c ∈ {1,2,4,5,6,8}\{a,b}.
Suy ra trong trường hợp này có 1.6.5.4 = 120 số.
TH2: d ≠ 0, d chẵn nên d ∈ {2,4,6,8}. Vậy có 4 cách chọn d
Với mỗi cách chọn d, do a ≠ 0 nên ta có 5 cách chọn a ∈ {1,2,4,5,6,8}\{d}.
Với mỗi cách chọn a,d ta có 5 cách chọn b ∈ {0,1,2,4,5,6,8}\{a,d}.
Với mỗi cách chọn a, b, d ta có 4 cách chọn c ∈ {0,1,2,4,5,6,8}\{a,d,b}.
Suy ra trong trường hợp này có 4.5.5.4= 400 số.
Vậy có tất cả 120 + 400 = 520 số cần lập.
Bài 21: Một hội đồng gồm 2 giáo viên và 3 học sinh được chọn từ một nhóm 5 giáo viên và 6 học sinh. Hỏi có bao nhiêu cách chọn?
A.200. B. 150. C.160. D.180.
Lời giải:
Đáp án: A
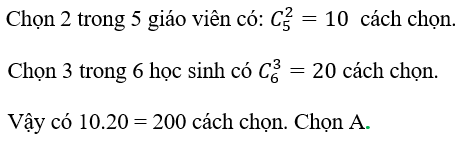
Bài 22: Nếu một đa giác đều có 44 đường chéo, thì số cạnh của đa giác là:
A. 11. B.10. C.9. D.8.
Lời giải:
Đáp án: A
Cứ hai đỉnh của đa giác n (n ∈ N, n ≥ 3) đỉnh tạo thành một đoạn thẳng (bao gồn cả cạnh đa giác và đường chéo).
Khi đó số đường chéo là:
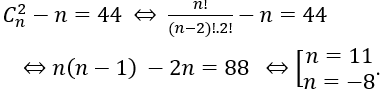
Vậy số cạnh của đa giác đó là 11. Chọn A.
Bài 23: Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là:
Lời giải:
Đáp án: A
Số tập con có 3 phần tử của một tập hợp có 7 phần tử là số tổ hợp chập 3 của 7. Vậy chọn A.
Bài 24: Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ:
A. 6. B. 72. C. 720. D.144.
Lời giải:
Đáp án: B
Chọn vị trí 3 nam và 3 nữ: 2.1 cách chọn.
Xếp 3 nam có: 3.2.1 cách xếp.
Xếp 3 nữ có: 3.2.1 cách xếp.
Vậy có 2.1.(3.2.1)2 = 72 cách xếp. Chọn B.
Bài 25: Từ các số 1,2,3,4,5,6,7 lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số chẵn
A. 360 B. 343 C. 523 D. 347
Lời giải:
Đáp án: A
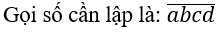
(a ≠ 0,a,b,c,d ∈ {1,2,3,5,4,6,7}) và a,b,c,d đôi một khác nhau.
Công việc ta cần thực hiện là lập số x thỏa mãn x là số chẵn nên d phải là số chẵn. Do đó để thực hiện công việc này ta thực hiện qua các công đoạn sau
Bước 1: Chọn d: Vì d là số chẵn nên d chỉ có thể là các số 2, 4, 6 nên d có 3 cách chọn.
Bước 2: Chọn a: Vì ta đã chọn d nên a chỉ có thể chọn một trong các số của tập {1,2,3,5,4,6,7}\{d} nên có 6 cách chọn a
Bước 3: Chọn b: Tương tự ta có 5 cách chọn b
Bước 4: Chọn c: Có 4 cách chọn.
Vậy theo quy tắc nhân có: 3.6.5.4 = 360 số thỏa yêu cầu bài toán. Chọn A.
Bài 26: Một tổ gồm 12 học sinh trong đó có bạn An. Hỏi có bao nhiêu cách chọn 4 em đi trực trong đó phải có An:
A. 990. B. 495. C.220. D.165.
Lời giải:
Đáp án: D
Chọn An có 1 cách chọn.
Chọn 3 bạn trong 11 bạn còn lại có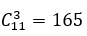 
cách chọn.
Vậy có 165 cách chọn. Chọn D.
Bài 27: Một đa giác đều có số đường chéo gấp đôi số cạnh. Hỏi đa giác đó có bao nhiêu cạnh?
A. 5. B. 6. C.7. D.8.
Lời giải:
Đáp án: C
Đa giác có n (n ∈ N,n ≥ 3).
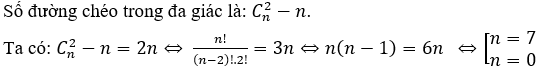
Vậy số cạnh của đa giác đó là 7. Chọn C.
Bài 28: Cho biết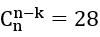 
. Giá trị của n và k lần lượt là:
A.8 và 4. B. 8 và 3.
C. 8 và 2. D. Không thể tìm được.
Lời giải:
Đáp án: C
Chọn C.
Thử đáp án, dễ dàng tìm được n=8 và k=2.
Bài 29: Số điện thoại ở Huyện Củ Chi có 7 chữ số và bắt đầu bởi 3 chữ số đầu tiên là 790. Hỏi ở Huyện Củ Chi có tối đa bao nhiêu máy điện thoại:
A. 1000. B.100000. C.1000. D.1000000.
Lời giải:
Đáp án: C
Gọi số điện thoại cần tìm có dạng 
Khi đó: a có cách 10 chọn, b có 10 cách chọn, c có 10 cách chọn, d có 10 cách chọn.
Nên có tất cả 10.10.10.10.10 = 104 số. Chọn C
Bài 30: Từ các số 1,2,3,4,5,6,7 lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số lẻ
A. 360 B. 343 C. 480 D. 347
Lời giải:
Đáp án: C
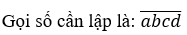
(a ≠ 0,a,b,c,d ∈ {1,2,3,5,4,6,7}) và a,b,c,d đôi một khác nhau.
Vì số x cần lập là số lẻ nên d phải là số lẻ. Ta lập x qua các công đoạn sau.
Bước 1: Có 4 cách chọn d
Bước 2: Có 6 cách chọn a
Bước 3: Có 5 cách chọn b
Bước 4: Có 4 cách chọn c
Vậy có 480 số thỏa yêu cầu bài toán. Chọn C.
Bài 31: Từ một nhóm 5 người, chọn ra các nhóm ít nhất 2 người. Hỏi có bao nhiêu cách chọn:
A. 25. B.26. C.31. D.32.
Lời giải:
Đáp án: B
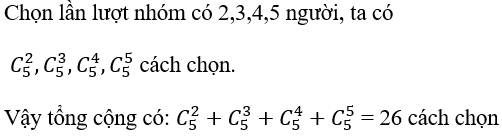
Bài 32: Mười hai đường thẳng có nhiều nhất bao nhiêu giao điểm?
A. 12. B. 66. C.132. D. 144.
Lời giải:
Đáp án: B
Chọn B.
Để được nhiều giao điểm nhất thì mười hai đường thẳng này phải đôi một cắt nhau tại các điểm phân biệt.
Như vậy có 
Bài 33: Kết quả nào sau đây sai:
Lời giải:
Đáp án: C
Chọn C.
Vì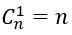 
nên câu C sai
Bài 34: Có bao nhiêu cách xếp 4 người A,B,C,D lên 3 toa tàu, biết mỗi toa có thể chứa 4 người.
A. 81 B. 68 C. 42 D. 98
Lời giải:
Đáp án: A
Để xếp A ta có 3 cách lên một trong ba toa
Với mỗi cách xếp A ta có 3 cách xếp B lên toa tàu
Với mỗi cách xếp A,B ta có 3 cách xếp C lên toa tàu
Với mỗi cách xếp A,B,C ta có 3 cách xếp D lên toa tàu
Vậy có 3.3.3.3 = 81 cách xếp 4 người lên toa tàu. Chọn A
Bài 35: Có bao nhiêu số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị?
A. 40. B.45. C. 50. D. 55.
Lời giải:
Đáp án: B
Nếu chữ số hàng chục là n thì số hàng đơn vị phải nhỏ hơn hoặc bằng n – 1. Vậy chọn chữ số hàng đơn vị có n – 1 cách. Mà chữ số hàng chục lớn hơn bằng bằng 1 nên ta có số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là: 1 + 2 + 3 + 4 + 5 +6 +7+8+9 = 45 nên chọn B.
Bài 36: Số cách chọn một ban chấp hành gồm một trưởng ban, một phó ban, một thư kí và một thủ quỹ được chọn từ 16 thành viên là:
Lời giải:
Đáp án: D
Chọn 4 trong 16 thành viên để bầu ban chấp hành (có phân biệt thứ tự) có 
Bài 37: Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt (n ≥ 2 ). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 20 B. 21 C. 30 D. 32
Lời giải:
Đáp án: A
Chọn A.
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d1 và hai đỉnh thuộc d2. Loại này có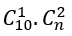 
tam giác.
Loại 2: Tam giác có một đỉnh thuộc d2 và hai đỉnh thuộc d1. Loại này có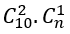 
tam giác.
Theo bài ra ta có:
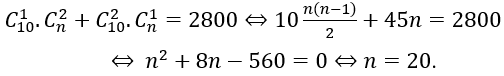
Bài 38: Tổng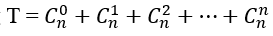 
bằng:
A. T = 2n. B. T = 2n-1. C. T = 2n+1. D. T = 4n.
Lời giải:
Đáp án: A
Chọn A.
Tính chất của khai triển nhị thức Niu – Tơn.
Bài 39: Có 3 nam và 3 nữ cần xếp ngồi vào một hàng ghế. Hỏi có mấy cách xếp sao cho nam, nữ ngồi xen kẽ và có một người nam A, một người nữ B phải ngồi kề nhau ?
A. 40 B. 42 C. 46 D. 70
Lời giải:
Đáp án: A
Cho cặp nam nữ A, B đó ngồi vào chỗ thứ nhất và chỗ thứ hai, có 2 cách. Tiếp đến, chỗ thứ ba có 2 cách chọn, chỗ thứ tư có 2 cách chọn, chỗ thứ năm có 1 cách chọn, chỗ thứ sáu có 1 cách chọn.
Bây giờ, cho cặp nam nữ A, B đó ngồi vào chỗ thứ hai và chỗ thứ ba. Khi đó, chỗ thứ nhất có 2 cách chọn, chỗ thứ tư có 2 cách chọn, chỗ thứ năm có 1 cách chọn, chỗ thứ sáu có 1 cách chọn.
Tương tự khi cặp nam nữ A, B đó ngồi vào chỗ thứ ba và thứ tư, thứ tư và thứ năm, thứ năm và thứ sáu.
Vậy có : 5.2.2.2.1.1 = 40 cách. Chọn A.
Bài 40: Có bao nhiêu số tự nhiên có 3 chữ số:
A. 900. B. 901. C. 899. D. 999.
Lời giải:
Đáp án: A
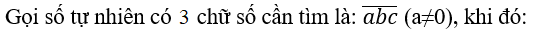
a có 9 cách chọn
b có 10 cách chọn
c có 10 cách chọn
Vậy có: 9.10.10 = 900 số
Nên chọn A.
Bài 41: Trong một buổi hoà nhạc, có các ban nhạc của các trường đại học từ Huế, Đà Nằng, Quy Nhơn, Nha Trang, Đà Lạt tham dự. Tìm số cách xếp đặt thứ tự để các ban nhạc Nha Trang sẽ biểu diễn đầu tiên.
A.4. B.20. C.24. D.120.
Lời giải:
Đáp án: B
Sắp xếp thứ tự biểu diễn của 4 ban nhạc còn lại có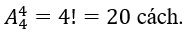 
Chọn B.
Bài 42: Giải bất phương trình (ẩn n thuộc tập số tự nhiên)
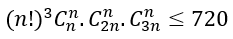
A. n=1,2,3 B. n=0,1,2 C. n=0,2,3 D. n=2,3,4
Lời giải:
Đáp án: B
Chọn B.
Điều kiện n ∈ ,n ≥ 0.
Với điều kiện đó bất phương trình tương đương
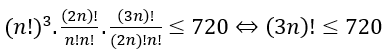
Ta thấy (3n)! tăng theo n và mặt khác 6!=720 ≥ (3n)!
Suy ra bất phương trình có nghiệm n=0,1,2.
Bài 43: Giải bất phương trình (ẩn n thuộc tập số tự nhiên)
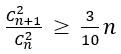
A. 2 ≤ n<4 B. 0 ≤ n ≤ 2 C. 1 ≤ n ≤ 5 D. 2 ≤ n ≤ 5
Lời giải:
Đáp án: D
Chọn D.
Bài 44: Có 3 nam và 3 nữ cần xếp ngồi vào một hàng ghế. Hỏi có mấy cách xếp sao cho nam, nữ ngồi xen kẽ và có một người nam C, một người nữ D không được ngồi kề nhau ?
A. 32 B. 30 C. 35 D. 70
Lời giải:
Đáp án: A
Số cách chọn để cặp nam nữ đó không ngồi kề nhau bằng số cách chọn tuỳ ý trừ số cách chọn để cặp nam nữ đó ngồi kề nhau.
Vậy có : 70 – 40 = 32 cách.Chọn A
Bài 45: Cho các chữ số 1, 2, 3,., 9. Từ các số đó có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau và không vượt quá 2011.
A. 168 B. 170 C. 164 D. 172
Lời giải:
Đáp án: A
Gọi số cần lập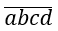 
(a ≠ 0,a,b,c,d ∈ {1,2,3,5,4,6,7,8,9})
Vì x chẵn nên d ∈ {2,4,6,8}. Đồng thời x ≤ 2011 ⇒ a = 1
a = 1 nên a có 1 cách chọn, khi đó d có 4 cách chọn.
Chọn b có 7 cách và chọn c có 6 cách.
Suy ra có: 1.4.6.7 = 168 số. Chọn A.
Bài 46: Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọc. Có bao nhiêu cách xếp hàng khác nhau nếu ông An hay bà An đứng ở đầu hoặc cuối hàng:
A.720. B. 1440. C.18720. D.40320.
Lời giải:
Đáp án: C
Ta dùng phần bù.
Sắp 8 người vào 8 vị trí theo hàng dọc có 8! cách sắp xếp.
Sắp ông và bà An vào 2 trong 6 vị trí (trừ vị trí đầu và cuối hàng) có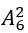 
cách.
Sắp 6 người con vào 6 vị trí còn lại có 6! cách.
Vậy có 8! - 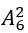.6!=18720.
Chọn C.
Bài 47:
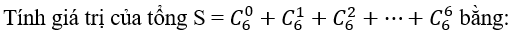
A. 64. B.48. C.72. D.100
Lời giải:
Đáp án: A
Chọn A.
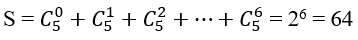
Bài 48: Trong khai triển (2x-5y)8, hệ số của số hạng chứa x5.y3 là:
A. -22400. B.-40000. C. -8960. D.-4000.
Lời giải:
Đáp án: A
Chọn A
Số hạng tổng quát trong khai triển trên là
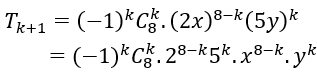
Yêu cầu bài toán xảy ra khi k=3. Khi đó hệ số của số hạng chứa x5.y3 là:-22400.
Bài 49: Trong khai triển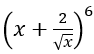 
, hệ số của x3,(x > 0) là:
A. 60. B. 80 C. 160. D. 240.
Lời giải:
Đáp án: C
Chọn C.
Số hạng tổng quát trong khai triển trên là
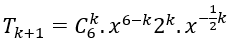
Yêu cầu bài toán xảy ra khi 6-k-1/2 k=3 ⇔ =3.
Khi đó hệ số của x3 là:
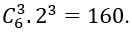
Bài 50: Khai triển (x+y)5 rồi thay x, y bởi các giá trị thích hợp.
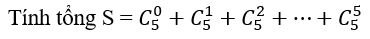
A. 32. B.64. C.1. D.12.
Lời giải:
Đáp án: A
Chọn A.
Với x = 1, y = 1 ta có
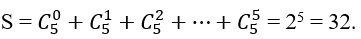
Bài 51: Trong một hộp bánh có 6 loại bánh nhân thịt và 4 loại bánh nhân đậu xanh. Có bao nhiêu cách lấy ra 6 bánh để phát cho các em thiếu nhi.
A. 240 B.151200. C.14200. D.210.
Lời giải:
Đáp án: D
Chọn 6 trong 10 bánh có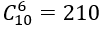 
cách. Chọn D.
Bài 52: Trong khai triển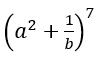 
, số hạng thứ 5 là:
A. 35.a6.b(-4). B. -35.a6.b(-4). C.35.a4.b(-5). D.-35.a4.b.
Lời giải:
Đáp án: A
Chọn A.
Số hạng tổng quát trong khai triển trên là
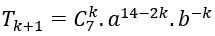
Vậy số hạng thứ 5 là
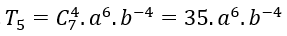
Bài 53:
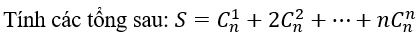
A. 2n. 2(n-1) B. n. 2(n+1) C. 2n. 2(n+1) D. n. 2(n-1)
Lời giải:
Đáp án: D
Chọn D.
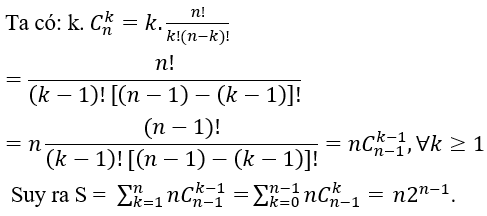
Bài 54: Trong khai triển (2a-1)6, tổng ba số hạng đầu là:
A.2a6-6a5+15a4. B. 2a6-15a5+30a4.
C.64a6-192a5+480a4. D. 62a6-192a5+240a4.
Lời giải:
Đáp án: D
Chọn D.
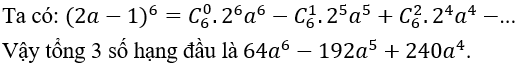
Bài 55: Tìm số nguyên dương n sao cho:
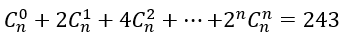
A. 4 B. 11 C. 12 D. 5
Lời giải:
Đáp án: D
Chọn D.
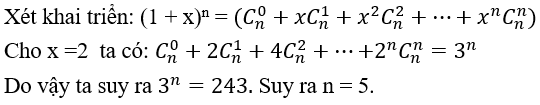
Bài 56: Một Thầy giáo có 10 cuốn sách Toán đôi một khác nhau, trong đó có 3 cuốn Đại số, 4 cuốn Giải tích và 3 cuốn Hình học. Ông muốn lấy ra 5 cuốn và tặng cho 5 học sinh sao cho sau khi tặng mỗi loại sách còn lại ít nhất một cuốn. Hỏi có bao nhiêu cách tặng.
A. 23314 B. 32512 C. 24480 D. 24412
Lời giải:
Đáp án: C
Số cách lấy 5 cuốn sách và đem tặng cho 5 học sinh:
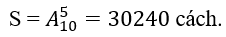
Số cách chọn sao cho không còn sách Đại số:
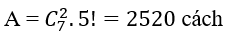
Số cách chọn sao cho không còn sách Giải tích:
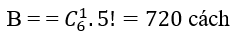
Số cách chọn sao cho không còn sách Hình học:
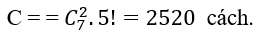
Vậy số cách tặng thỏa yêu cầu bài toán: S – A – B – C = 24480 cách tặng. Chọn C
Bài 57: Trong khai triển (x-√y)16, tổng hai số hạng cuối là:
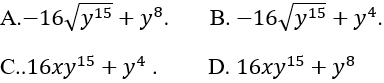
Lời giải:
Đáp án: A
Chọn A.
Ta có:
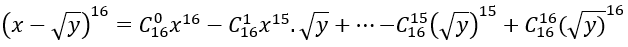
Bài 58: Trong khai triển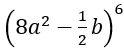 
, hệ số của số hạng chứa a9 b3 là:
A. -80a9 b3. B. -64a9 b3. C. -1280a9 b3. D. 60a6 b4.
Lời giải:
Đáp án: C
Chọn C.
Số hạng tổng quát trong khai triển trên là 
Yêu cầu bài toán xảy ra khi k=3.
Khi đó hệ số của số hạng chứa a9 b3 là: -1280a9 b3.
Bài 59:
Lời giải:
Đáp án: B
Chọn B.
Ta có:
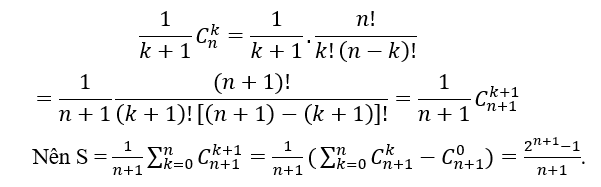
Bài 60: Một đội thanh niên tình nguyện có 15 người,gồm 12 nam và 3 nữ.Hỏi có bao nhiêu cách phân công đội thanh niên tình nguyện đó về giúp đỡ 3 tỉnh miền núi, sao cho mỗi tỉnh có 4 nam và một nữ ?
A. 12141421 B. 5234234 C. 4989600 D. 4144880
Lời giải:
Đáp án: C
Có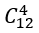 
cách phân công 4 nam về tỉnh thứ nhất
Với mỗi cách phân công trên thì có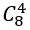 
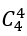
cách phân công 4 nam về tỉnh thứ hai và có 
cách phân công 4 nam còn lại về tỉnh thứ ba.
Khi phân công nam xong thì có 3! cách phân công ba nữ về ba tỉnh đó.
Vậy có tất cả 
cách phân công. Chọn C.
