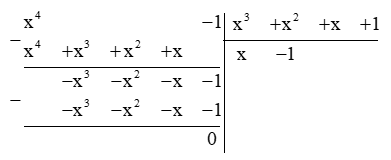Cho P(x) = x^3 + x^2 + x + 1 và Q(x) = x^4 – 1

Cho P(x) = x + x + x + 1 và Q(x) = x – 1

Giải vở bài tập Toán 7 Bài tập cuối chương 6

Câu 9 trang 64 vở bài tập Toán lớp 7 Tập 2: Cho P(x) = x³ + x² + x + 1 và Q(x) = x⁴ – 1

a) Tính P(x).Q(x)

b) Tìm đa thức A(x) sao cho P(x).A(x) = Q(x).

Lời giải:

a) P(x).Q(x) = (x³ + x² + x + 1).(x⁴ – 1)

= ( x³.x⁴ + x².x⁴ + x.x⁴ + x⁴) – 1. ( x³ + x² + x + 1)

= x⁷ + x⁶ + x⁵ + x⁴ – x³ – x² – x – 1.

b) P(x).A(x) = Q(x)

⇒ A(x) = Q(x) : P(x)

⇔ A(x) = (x⁴ – 1) : (x³ + x² + x + 1)

Vậy A(x) = x – 1.