Giải Vở bài tập Toán 7 trang 104 Tập 2 Cánh diều

---

Với Giải VBT Toán 7 trang 104 Tập 2 trong Bài 9: Đường trung trực của một đoạn thẳng Vở bài tập Toán lớp 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VBT Toán 7 trang 104.

Giải VBT Toán 7 trang 104 Tập 2 Cánh diều

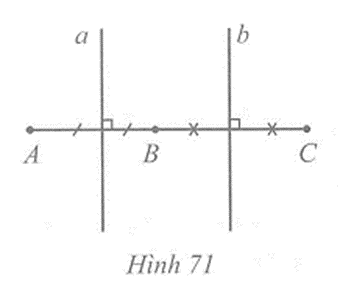
Câu 3 trang 104 vở bài tập Toán lớp 7 Tập 2: Cho ba điểm A, B, C thẳng hàng, điểm B nằm giữa hai điểm A và C. Gọi a, b lần lượt là đường trung trực của đoạn thẳng AB và BC. Chứng minh rằng a // b.

Lời giải:

- Vì a là đường trung trực của đoạn thẳng AB nên a $\perp$ AB (tính chất đường trung trực) suy ra a ⊥ AC.

- Vì b là đường trung trực của đoạn thẳng BC nên b $\perp$ BC (tính chất đường trung trực) suy ra b ⊥ AC.

Vì a và b cùng vuông góc với AC nên a // b.

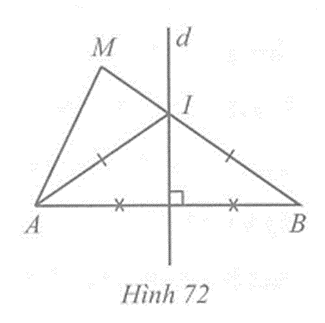
Câu 4 trang 104 vở bài tập Toán lớp 7 Tập 2: Cho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M không thuộc đường thẳng d và đoạn thẳng AB sao cho đường thẳng d cắt đoạn thẳng MB tại điểm I. Chứng minh:

a) MB = AI + IM;

b) MA < MB.

Lời giải:

a) Vì điểm I thuộc đường thẳng trung trực của đoạn thẳng AB nên AI = BI.

Do đó: MB = BI + IM = AI + IM

b) Xét tam giác MIA, ta có MA < AI + IM (bất đẳng thức tam giác)

mà AI + IM = MB (chứng minh trên), suy ra MA < MB.

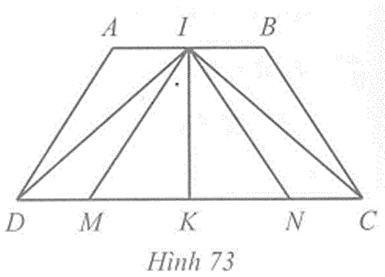
Câu 5 trang 104 vở bài tập Toán lớp 7 Tập 2: Cho hình thang ABCD có AB song song với CD, AB < CD, AD = BC. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD. Đường thẳng qua I song song với AD cắt đoạn thẳng KD tại M. Đường thẳng qua I song song với BC cắt KC tại N Hình 73. Chứng minh:

a) IM = IN;

b) IK là đường trung trực của hai đoạn thẳng AB và CD.

Lời giải:

Vẽ các đoạn thẳng IC, ID. Xét hai tam giác ADI và MID, ta có

$\widehat{\mathrm{ADI}}$= $\widehat{\mathrm{DIM}}$ (hai góc so le trong);

ID là cạnh chung;

$\widehat{\mathrm{AID}}$= $\widehat{\mathrm{IDM}}$(hai góc so le trong).

Suy ra ∆ADI = ∆MID (g.c.g). Do đó AD = MI, IA = DM (các cặp cạnh tương ứng)

Chứng minh tương tự ta có BC = IN, IB = NC

a) Vì AD = BC, AD = MI, BC = IN nên IM = IN.

b) Vì IA = IB, IA = DM, IB = CN nên DM = CN. Mà KC = KD nên KM = KN.

Vì IM = IN và KM = KN nên IK là đường trung trực của đoạn thẳng MN.

Suy ra IK $\perp$ MN. Do đó IK $\perp$ CD. Mà AB // CD nên IK $\perp$ AB.

Vì IK $\perp$ CD, KC = KD nên IK là đường trung trực của đoạn thẳng CD.

Vì IK $\perp$ AB, IA = IB nên IK là đường trung trực của đoạn thẳng AB.

Lời giải Vở bài tập Toán 7 Bài 9: Đường trung trực của một đoạn thẳng Cánh diều hay khác:

• Giải VBT Toán 7 trang 101 Tập 2

• Giải VBT Toán 7 trang 102 Tập 2

• Giải VBT Toán 7 trang 103 Tập 2