Giải Vở bài tập Toán 7 trang 106 Tập 2 Cánh diều

Với Giải VBT Toán 7 trang 106 Tập 2 trong Bài 10: Tính chất ba đường trung tuyến của tam giác Vở bài tập Toán lớp 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VBT Toán 7 trang 106.

Giải VBT Toán 7 trang 106 Tập 2 Cánh diều

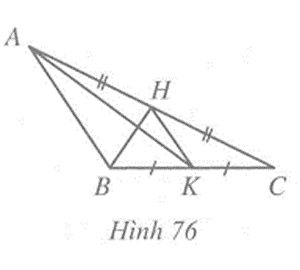
Câu 1 trang 106 vở bài tập Toán lớp 7 Tập 2: Trong Hình 76 đoạn thẳng HK là đường trung tuyến của tam giác nào?

Lời giải:

- Đoạn thẳng HK là đường trung tuyến của tam giác HBC vì H là một đỉnh của tam giác HBC và K là trung điểm của cạnh BC.

- Đoạn thẳng HK cũng là đường trung tuyến của tam giác AKC vì K là một đỉnh của tam giác AKC và H là trung điểm của cạnh AC.

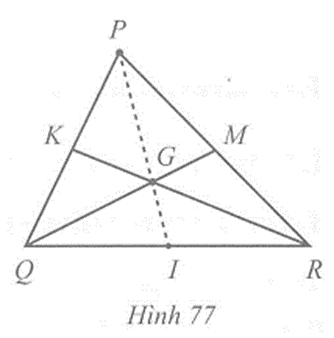
Câu 2 trang 106 vở bài tập Toán lớp 7 Tập 2: Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.

Lời giải:

Hai đường trung tuyến QM và RK cắt nhau tại G nên G là trọng tâm của tam giác PQR. Suy ra điểm G thuộc đường trung tuyến PI của tam giác PQR. Vậy ba điểm P, G, I thẳng hàng.

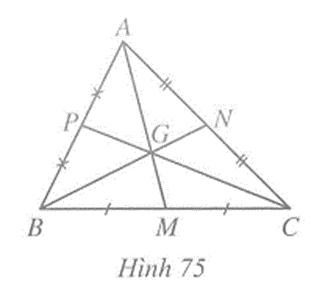
Câu 1 trang 106 vở bài tập Toán lớp 7 Tập 2: Cho tam giác ABC. Ba đường trung tyến AM, BN, CP đồng quy tại G. Chứng minh GA + GB + GC = $\frac{2}{3}$ (AM + BN + CP)

Lời giải:

Vì G là trọng tâm tam giác ABC nên GA = $\frac{2}{3}$ AM, GB = $\frac{2}{3}$BN, GC = $\frac{2}{3}$ CP.

Suy ra GA + GB + GC = $\frac{2}{3}$AM + $\frac{2}{3}$BN + $\frac{2}{3}$PC = $\frac{2}{3}$ (AM + BN + CP).

Vậy GA + GB + GC = $\frac{2}{3}$ (AM + BN + CP).

Lời giải Vở bài tập Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác Cánh diều hay khác:

• Giải VBT Toán 7 trang 105 Tập 2

• Giải VBT Toán 7 trang 107 Tập 2

• Giải VBT Toán 7 trang 108 Tập 2