Giải Vở bài tập Toán 7 trang 112 Tập 2 Cánh diều

❮ Bài trước Bài sau ❯

Với Giải VBT Toán 7 trang 112 Tập 2 trong Bài 11: Tính chất ba đường phân giác của tam giác Vở bài tập Toán lớp 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VBT Toán 7 trang 112.

Giải VBT Toán 7 trang 112 Tập 2 Cánh diều

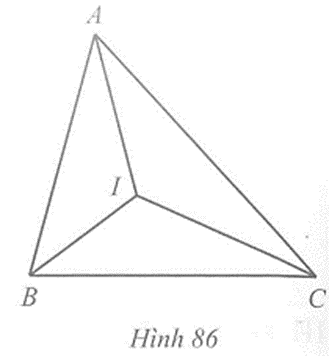
Câu 3 trang 112 vở bài tập Toán lớp 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.

a) Chứng minh $\hat{C B I}$ > $\hat{A C I}$ ;

b) So sánh IB và IC.

Lời giải:

Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC

a) Vì AB < AC nên $\hat{A C B}$ < $\hat{A B C}$ (1)

Vì các tia BI, CI lần lượt là tia phân giác của góc ABC và ACB nên

$\hat{C B I}$ = $\frac{1}{2}$ $\hat{A B C}$ và $\hat{A C I}$ = $\frac{1}{2}$ $\hat{A C B}$ (2)

Từ (1) và (2) suy ra $\hat{C B I}$ > $\hat{A C I}$

b) Ta có $\hat{C B I}$ > $\hat{A C I}$ ; $\hat{B C I}$ = $\hat{A C I}$ . Suy ra $\hat{C B I}$ > $\hat{B C I}$ .

Trong tam giác IBC, Vì $\hat{C B I}$ > $\hat{B C I}$ nên IC > IB hay IB < IC.

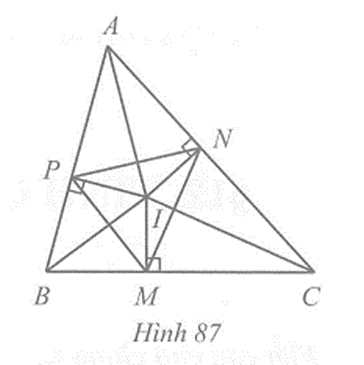
Câu 4 trang 112 vở bài tập Toán lớp 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của điểm I trên các cạnh BC, CA, AB. Chứng minh:

a) IA, IB, IC lần lượt là tia phân giác của các góc NIP, PIM, MIN.

b) $\hat{N I P}$ = 180^o – $\hat{B A C}$ ;

c) $\hat{I N P}$ = $\hat{I P N}$ = $\frac{1}{2}$ $\hat{B A C}$ ;

d) $\hat{M N P}$ = 90^o – $\frac{1}{2}$ $\hat{B A C}$ ;

Lời giải:

Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu

a) Xét hai tam giác vuông IAP và IAN, ta có:

IA là cạnh chung;

$\hat{I A P}$ = $\hat{I A N}$ (do I nằm trên tia phân giác góc A).

Suy ra ∆IAP = ∆IAM (cạnh huyền – góc nhọn).

Do đó $\hat{A I P}$ = $\hat{A I N}$ (hai góc tương ứng).

Suy ra tia IA là tia phân giác của góc NIP.

Chứng minh tương tự ta cũng có:

IB là tia phân giác của góc PIM, IC là tia phân giác của góc MIN.

b) Xét tam giác vuông AIP, ta có $\hat{A I P}$ + $\hat{I A P}$ = 90^o

Xét tam giác vuông AIN, ta có $\hat{A I N}$ + $\hat{I A N}$ = 90^o

Suy ra $\hat{A I P}$ + $\hat{I A P}$ + $\hat{A I N}$ + $\hat{I A N}$ = 90^o + 90^o = 180^o

( $\hat{A I P}$ + $\hat{A I N}$ ) + ( $\hat{I A P}$ + $\hat{I A N}$ ) = 180^o (1)

Mà $\hat{A I P}$ và $\hat{A I N}$ , $\hat{I A P}$ và $\hat{I A N}$ là các cặp góc kề nhau nên:

$\hat{A I P}$ + $\hat{A I N}$ = 90^o và $\hat{I A P}$ + $\hat{I A N}$ = 90^o (2)

Từ (1) và (2), suy ra: $\hat{N I P}$ + $\hat{N A P}$ = 180^o hay $\hat{N I P}$ + $\hat{B A C}$ = 180^o

Do đó: $\hat{N I P}$ = 180^o – $\hat{B A C}$ ;

c) Vì I là giao điểm của ba đường phân giác nên IN = IP

Suy ra tam giác INP là tam giác cân tại I. Do đó: $\hat{I N P}$ = $\hat{I P N}$

Mà $\hat{I N P}$ + $\hat{I P N}$ + $\hat{N I P}$ = 180^o (tổng ba góc của một tam giác)

Suy ra 2 $\hat{I N P}$ + (180^o – $\hat{B A C}$ ) = 180^o hay 2 $\hat{I N P}$ – $\hat{B A C}$ = 0^o.

Suy ra : $\hat{I N P}$ = $\hat{I P N}$ = $\frac{1}{2}$ $\hat{B A C}$ .

d) Chứng minh tương tự câu c, ta có: $\hat{I M P}$ = $\frac{1}{2}$ $\hat{A B C}$ , $\hat{I M N}$ = $\frac{1}{2}$ $\hat{A C B}$ .

Suy ra $\hat{N M P}$ = $\hat{I M P}$ + $\hat{I M N}$ = $\frac{1}{2}$ $\hat{A B C}$ + $\frac{1}{2}$ $\hat{A C B}$ = $\frac{1}{2}$ ( $\hat{A B C}$ + $\hat{A C B}$ ) (3)

Ta có $\hat{B A C}$ + $\hat{A B C}$ + $\hat{A C B}$ = 180^o (tổng ba góc của một tam giác)

Suy ra $\hat{A B C}$ + $\hat{A C B}$ = 180^o – $\hat{B A C}$

Từ (3) và (4) suy ra $\hat{N M P}$ = $\frac{1}{2}$ (180^o – $\hat{B A C}$ ) = 90^o – $\frac{1}{2}$ $\hat{B A C}$ .

Lời giải Vở bài tập Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác Cánh diều hay khác:

Xem thêm lời giải Vở bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

VBT Toán 7 Cánh diều

Giải Vở bài tập Toán 7 trang 112 Tập 2 Cánh diều

Giải VBT Toán 7 trang 112 Tập 2 Cánh diều

Xem thêm lời giải Vở bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: