Giải Vở bài tập Toán 7 trang 122 Tập 2 Cánh diều

---

Với Giải VBT Toán 7 trang 122 Tập 2 trong Bài 13: Tính chất ba đường cao của tam giác Vở bài tập Toán lớp 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VBT Toán 7 trang 122.

Giải VBT Toán 7 trang 122 Tập 2 Cánh diều

Câu 6 trang 122 vở bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đương trung trực. Chứng minh rằng:

a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau

b) Nếu tam giác ABC có hai điểm H, I trùng nhau thì tam giác ABC là tam giác đều.

Lời giải:

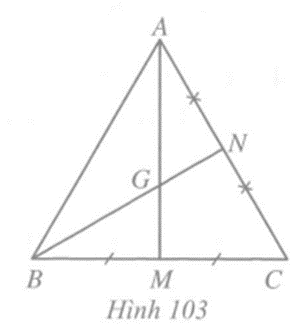
a) Hình 103

Vẽ đường trung tuyến AM, BN của tam giác ABC đều.

Xét hai tam giác AMB và AMC, ta có:

AM là cạnh chung;

AB = AC (tính chất của tam giác đều);

MB = MC (vì M là trung điểm của BC).

Suy ra ∆AMB = ∆AMC (c.c.c)

Do đó $\widehat{MAB}$ = $\widehat{MAC}$ và $\widehat{AMB}$ = $\widehat{AMC}$ (cặp góc tương ứng)

Do $\widehat{AMB}$ + $\widehat{AMC}$ = 180^o (hai góc kề bù) và $\widehat{AMB}$ = $\widehat{AMC}$ nên $\widehat{AMB}$ = $\widehat{AMC}$ = 90^o hay AM $\perp$ BC, suy ra AM là đường cao của tam giác ABC.

Vì AM $\perp$ BC, MB = MC nên AM là đường trung trực của tam giác ABC.

Vì $\widehat{MAB}$ = $\widehat{MAC}$ nên AM là đường phân giác góc A của tam giác ABC.

Như vậy, tam giác đều ABC có trung tuyến AM vừa là đường cao, vừa là đường trung trực, vừa là đường phân giác

Tương tự ta cũng chứng minh được tam giác đều ABC có đường trung tuyến BN vừa là đường cao, vừa là đường trung trực, vừa là đường phân giác.

Suy ra trọng tâm G của tam giác đều ABC đồng thời là giao điểm của ba đường phân giác, giao điểm của ba đường cao, giao điểm của ba đường trung trực.

Vậy nếu tam giác ABC đều thì bốn điểm G, H , I, O trùng nhau

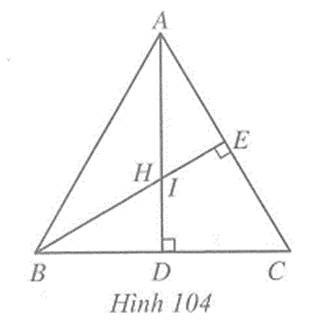
b) Hình 104

Vẽ hai đường cao AD, BE của tam giác ABC

Do H trùng với I nên AD, BE là hai đường phân giác của tam giác ABC

Xét hai tam giác vuông ADB và ADC, ta có:

AD là cạnh chung;

$\widehat{DAB}$ = $\widehat{DAC}$ (vì AD là đường phân giác của góc BAC).

Suy ra ∆ADB = ∆ADC (cạnh góc vuông – góc nhọn)

Do đó AB = AC (hai cạnh tương ứng). Chứng minh tương tự, ta có BC = BA

Suy ra AB = AC = BC

Vậy nếu tam giác ABC có hai điểm H, I trùng nhau thì tam giác ABC là tam giác đều.

Lời giải Vở bài tập Toán 7 Bài 13: Tính chất ba đường cao của tam giác Cánh diều hay khác:

• Giải VBT Toán 7 trang 118 Tập 2

• Giải VBT Toán 7 trang 119 Tập 2

• Giải VBT Toán 7 trang 120 Tập 2

• Giải VBT Toán 7 trang 121 Tập 2