Giải Vở bài tập Toán 7 trang 119 Tập 2 Cánh diều
Với Giải VBT Toán 7 trang 119 Tập 2 trong Bài 13: Tính chất ba đường cao của tam giác Vở bài tập Toán lớp 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VBT Toán 7 trang 119.
Giải VBT Toán 7 trang 119 Tập 2 Cánh diều
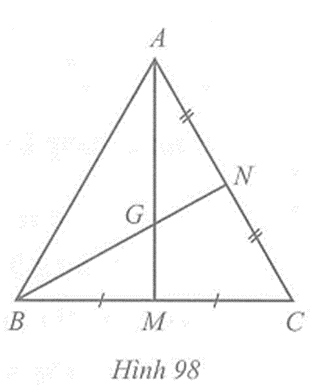
Câu 2 trang 119 vở bài tập Toán lớp 7 Tập 2: Cho tam giác đều ABC có trọng tâm G. Chứng minh G cũng là trực tâm của tam giác ABC
Lời giải:
Vẽ AM và BN là hai đường trung tuyến của tam giác ABC.
Vì tam giác ABC đều nên AB = AC, suy ra A thuộc đường trung trực của cạnh BC
Vì MB = MC nên M cũng thuộc đường trung trực của cạnh BC.
Do đó AM là đường trung trực của cạnh BC
Suy ra AM BC hay AM là đường cao của tam giác ABC
Chứng minh tương tự ta cũng có BN là đường cao của tam giác ABC.
Vì hai đường cao AM và BN cắt nhau tại G nên G là trực tâm của tam giác ABC.
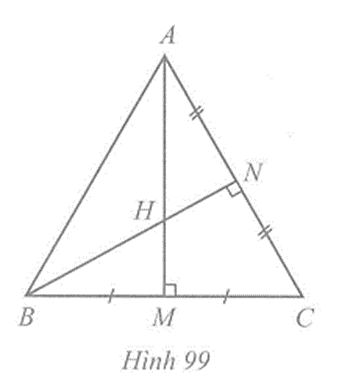
Câu 3 trang 119 vở bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều
Lời giải:
Vẽ AM và BN là hai đường trung tuyến của tam giác ABC.
Vì tam giác ABC có trực tâm H cũng là trọng tâm nên H là giao điểm của AM và BN.
Suy ra AM BC
Do M là trung điểm của BC và AM BC nên AM là đường trung trực của BC suy ra AB = AC.
Chứng minh tương tự ta có BA = BC.
Do đó AB = AC = BC. Vậy tam giác ABC là tam giác đều.
Lời giải Vở bài tập Toán 7 Bài 13: Tính chất ba đường cao của tam giác Cánh diều hay khác: