Giải Vở bài tập Toán 7 trang 121 Tập 2 Cánh diều

Với Giải VBT Toán 7 trang 121 Tập 2 trong Bài 13: Tính chất ba đường cao của tam giác Vở bài tập Toán lớp 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VBT Toán 7 trang 121.

Giải VBT Toán 7 trang 121 Tập 2 Cánh diều

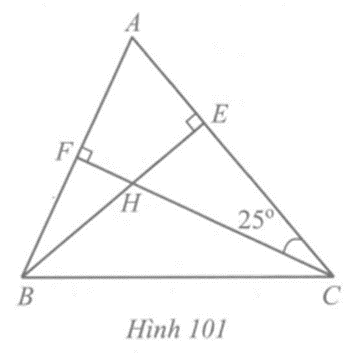
Câu 4 trang 121 vở bài tập Toán lớp 7 Tập 2: Cho tam giác nhọn ABC. Hai đường BE, CF cắt nhau tại H, $\widehat{\mathrm{HCA}}$ = 25^o. Tính $\widehat{BAC}$ và $\widehat{HBA}$.

Lời giải:

Xét tam giác ACF vuông tại F, ta có

$\widehat{FAC}$ + $\widehat{ACF}$ = 90^o (tổng hai góc nhọn trong tam giác vuông) hay $\widehat{BAC}$ + $\widehat{ACF}$ = 90^o

Suy ra $\widehat{BAC}$ = 90^o - $\widehat{ACF}$ = 90^o – 25^o = 75^o

Xét tam giác ABE vuông tại E, ta có

$\widehat{EBA}$ + $\widehat{BAE}$ = 90^o (tổng hai góc nhọn trong tam giác vuông) hay $\widehat{HBA}$ + $\widehat{BAC}$ = 90^o

Suy ra $\widehat{HBA}$ = 90^o – $\widehat{BAC}$ = 90^o – 75^o = 25^o.

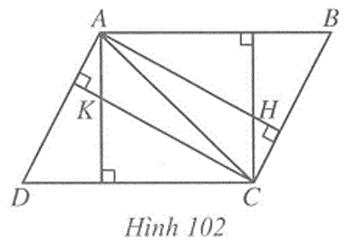
Câu 5 trang 121 vở bài tập Toán lớp 7 Tập 2: Trong Hình 102 cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm tam giác ABC và ACD. Chứng minh AK // CH và AH // CK

Lời giải:

Vì H là trực tâm của tam giác ABC nên CH ⊥ AB, AH ⊥ BC

Mà AB // CD, AD // BC suy ra CH ⊥ CD, AH ⊥ AD

Vì K là trực tâm tam giác ACD nên AK ⊥ CD, CK ⊥ AD

Do AK ⊥ CD, CH ⊥ CD nên AK // CH.

Do AH ⊥ AD, CK ⊥ AD nên AH // CK.

Lời giải Vở bài tập Toán 7 Bài 13: Tính chất ba đường cao của tam giác Cánh diều hay khác:

• Giải VBT Toán 7 trang 118 Tập 2

• Giải VBT Toán 7 trang 119 Tập 2

• Giải VBT Toán 7 trang 120 Tập 2

• Giải VBT Toán 7 trang 122 Tập 2