Giải Vở bài tập Toán 7 trang 124 Tập 2 Cánh diều

---

Với Giải VBT Toán 7 trang 124 Tập 2 trong Bài tập cuối chương 7 Vở bài tập Toán lớp 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VBT Toán 7 trang 124.

Giải VBT Toán 7 trang 124 Tập 2 Cánh diều

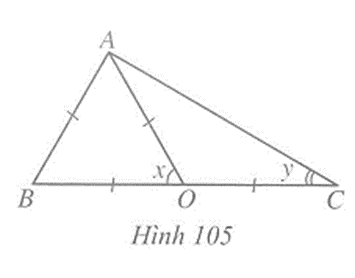
Câu 2 trang 124 vở bài tập Toán lớp 7 Tập 2: Tính các số đo x, y trong Hình 105

Lời giải:

Vì AB = OA = OB nên tam giác ABO là tam giác đều. Suy ra x = 60^o.

Do x + $\widehat{AOC}$ = 180^o (hai góc kề bù) nên $\widehat{AOC}$ = 180^o – x = 180^o – 60^o = 120^o.

Ta có $\widehat{AOC}$ + $\widehat{OAC}$ + $\widehat{ACO}$ = 180^o (tổng ba góc của một tam giác)

Vì OA = OC nên tam giác AOC là tam giác cân tại O

Do đó $\widehat{OAC}$ = $\widehat{OCA}$ = y

Từ đó suy ra $\widehat{AOC}$ + 2y = 180^o hay y = $\frac{{180}^o-\widehat{AOC}}{2}=\frac{{180}^o-{120}^o}{2}=30°$.

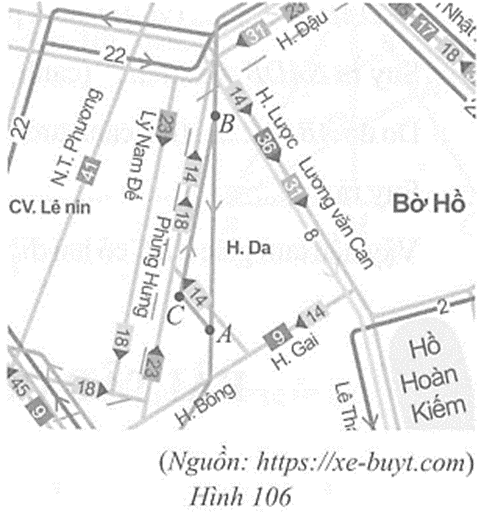
Câu 3 trang 124 vở bài tập Toán lớp 7 Tập 2: Bạn Hoa đánh dấu ba vị trí A, B, C trên một phần sơ đồ xe buýt ở Hà Nội năm 2021 và xem xe buýt có thể đi như thế nào giữa hai vị trí A và B. Đường thứ nhất đi từ A đến C và đi tiếp từ C đến B, đường thứ hai đi từ B đến A (Hình 106). Theo em đường nào đi dài hơn? Vì sao?

Lời giải:

Xét tam giác ABC ta có

AC + CB > AB (bất đẳng thức tam giác).

Do đó đường đi thứ nhất dài hơn đường đi thứ hai.

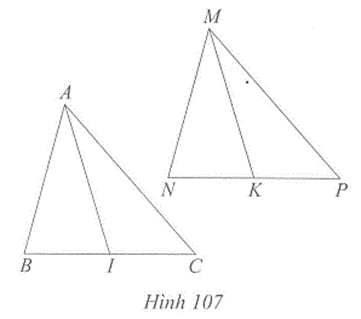
Câu 4 trang 124 vở bài tập Toán lớp 7 Tập 2: Cho hai tam giác ABC và MNP có:

AB = MN, BC = NP, CA = PM. Gọi I và K lần lượt là trung điểm của BC và NP. Chứng minh AI = MK.

Lời giải:

Xét hai tam giác ABC và MNP, ta có:

AB = MN, BC = NP, CA = PM

Suy ra ∆ABC = ∆MNP (c.c.c)

Do đó $\hat{B}$ = $\hat{N}$ (hai góc tương ứng)

Vì I là trung điểm của BC nên BI = $\frac{1}{2}$BC

Vì K là trung điểm của NP nên NK = $\frac{1}{2}$NP

Mà BC = NP, suy ra BI = NK

Xét hai tam giác ABI và MNK, ta có:

AB = MN, $\hat{B}$ = $\hat{N}$ ; BI = NK

Suy ra ∆ABI = ∆MNK (c.g.c)

AI = MK (hai cạnh tương ứng)

Lời giải Vở bài tập Toán 7 Bài tập cuối chương 7 Cánh diều hay khác:

• Giải VBT Toán 7 trang 123 Tập 2

• Giải VBT Toán 7 trang 125 Tập 2

• Giải VBT Toán 7 trang 126 Tập 2

• Giải VBT Toán 7 trang 127 Tập 2

• Giải VBT Toán 7 trang 128 Tập 2

• Giải VBT Toán 7 trang 129 Tập 2

• Giải VBT Toán 7 trang 130 Tập 2

• Giải VBT Toán 7 trang 131 Tập 2